Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

* Xét tứ giác ABCD, ta có:
MA = MC (gt)
MB = MD (định nghĩa đối xứng tâm)
Suy ra: Tứ giác ABCD là hình bình hành (vì có hai đường chéo cắt nhau tại trung điểm của mỗi đường)
⇒ AD // BC và AD = BC (1)
* Xét tứ giác ACBE, ta có:
AN = NB (gt)
NC = NE (định nghĩa đối xứng tâm)
Suy ra: Tứ giác ACBE là hình bình hành (vì có 2 đường chéo cắt nhau tại trung điểm của mỗi đường) ⇒ AE // BC và AE = BC (2)
Từ (1) và (2) suy ra: A, D, E thẳng hàng và AD = AE
Nên A là trung điểm của DE hay điểm D đối xứng với điểm E qua điểm A.

a: Xét tứ giác ABCD có
M là trung điểm của AC
M là trung điểm của BD
Do đó: ABCD là hình bình hành
a. Vì tam giác ABC có trung tuyến BM (gt)
-> M là trung điểm AC
Vì D đối xứng với B qua M (gt)
-> M là trung điểm BD
xét tứ giác ABCD có : - M là trung điểm AC (cmt)
- M là trung điểm BD (cmt)
=> tứ giác ABCD là hình bình hành
b) Vì tam giác ABC có trung tuyến CN(gt)
-> N là trung điểm AB
Vì E đối xứng với C qua N (gt)
-> N là trung điểm EC
xét tứ giác AEBC có : - N là trung điểm AB (cmt)
- N là trung điểm EC (cmt)
-> tứ giác AEBC là hình bình hành
=> AE // BC ( tính chất )
c)Vì tứ giác ABCD là hình bình hành ( cmt )
-> AD = BC (tính chất) (1)
Vì tứ giác AEBC là hình bình hành ( cmt )
-> AE = BC (2)
từ (1) và (2) => AE = AD
=> A là trung điểm ED
=> E đối xứng vói D qua A

a, Vì N là trung điểm BD và AC nên ABCD là hbh
Vì M là trung điểm CE và AB nên AEBC là hbh
b, Vì ABCD và AEBC là hbh nên \(\left\{{}\begin{matrix}AE//BC;AE=BC\\AD//BC;AD=BC\end{matrix}\right.\Rightarrow AE\equiv AD;AE=AD\)
Vậy E đx D qua A

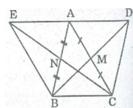
* Xét tứ giác ABCD, ta có:
MA = MC (gt)
MB = MD (định nghĩa đối xứng tâm)
Suy ra: Tứ giác ABCD là hình bình hành (vì có hai đường chéo cắt nhau tại trung điểm của mỗi đường)
⇒ AD // BC và AD = BC (1)
* Xét tứ giác ACBE, ta có:
AN = NB (gt)
NC = NE (định nghĩa đối xứng tâm)
Suy ra: Tứ giác ACBE là hình bình hành (vì có 2 đường chéo cắt nhau tại trung điểm của mỗi đường) ⇒ AE // BC và AE = BC (2)
Từ (1) và (2) suy ra: A, D, E thẳng hàng và AD = AE
Nên A là trung điểm của DE hay điểm D đối xứng với điểm E qua điểm A.
xét tam giác ADE có:
AB=DB( gt)
AC=EC (gt)
=> BC//DE ( t/c đường trung bình)
ta có: BC//DE (CMT)
AM vuông góc với BC
AM=IM
=> góc AID= góc AIE
Xét tam giác AEI và tam giác ADIcó:
góc DAI= góc EAI
AI chung
góc AID= góc AIE (CMT)
=> tam giác AEI = tam giác ADI (g.c.g)
=> DI=EI(2 cạnh tương ứng)

Xét tứ giác ABCD có
AM=CM; BM=DM => ABCD là hình bình hành (tứ giác có 2 đường chéo cắt nhau tại trung điểm mỗi đường là hbh)
=> AD//=BC
Xét ứ giác ACBE có
AN=BN; CN=EN => ACBE là hình bình hành (tứ giác có 2 đường chéo cắt nhau tại trung điểm mỗi đường là hbh)
=> AE//=BC
=> AD=AE =BC
=> AE trùng AD hay A; D; E thẳng hàng (Qua 1 điểm ngoài đường thẳng chỉ dựng được duy nhất 1 đường thẳng // với đường thẳng đã cho)
=> D đối xứng với E qua A

a, hai đường chéo cắt nhau tại trung điểm mỗi đường
b, DM là đường trung bình của tam giác ABC nên DM song song AC hay EM song song với AC mà AB vuông góc với AC nên EM vuông góc với AB
c, ta có DM là dường trung bình của tam giác ABC nên DM bằng 1 phần 2 AC mà DM bằng 1/2 EM nên EM=AC mà EM//AB nên EAMC là hình bình hành nên F là trung điểm EC nên E,F,C thẳng hàng

a: Xét tứ giác ABCD có
M là trung điểm chung của AC và BD
nên ABCD là hình bình hành
b: Xét tứ giác AEBC có
N là trung điểm chung của AB và EC
nên AEBC là hình bình hành
=>AE//BC và AE=BC
=>AD//AE và AD=AE
=>A là trung điểm của DE

1: Xét tứ giác ABCD có
M là trung điểm của AC
M là trung điểm của BD
Do đó: ABCD là hình bình hành