Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Lời giải:
a)
Theo định lý tổng 3 góc trong tam giác:
$\widehat{D}+\widehat{E}+\widehat{F}=180^0$
$\Rightarrow \widehat{E}+\widehat{F}=180^0-\widehat{D}=180^0-60^0=120^0$
Mà tam giác $DEF$ cân tại $D$ nên $\widehat{E}=\widehat{F}$
Do đó:
$\widehat{E}=\widehat{F}=\frac{120^0}{2}=60^0$
b)
Xét tam giác $ABM$ và $ACM$ có:
$AB=AC$ (do $ABC$ cân tại $A$)
$\widehat{B}=\widehat{C}$ (do $ABC$ cân tại $A$)
$BM=CM$ (do $M là trung điểm $BC$)
$\Rightarrow \triangle ABM=\triangle ACM$ (c.g.c)

Answer:
a,
Ta có: \(\widehat{A}+\widehat{B}+\widehat{C}=180^o\)
Mà đề ra: \(\widehat{A}=40^o\)
\(\widehat{B}=\widehat{C}\) (Tam giác ABC cân tại A)
\(\Rightarrow40^o+\widehat{B}+\widehat{B}=180^o\)
\(\widehat{2B}=140^o\)
\(\widehat{B}=70^o\)
\(\Rightarrow\widehat{B}=\widehat{C}=70^o\)
C B A 40 độ
b,
Theo đề ra: Tam giác ABC cân tại A
\(\Rightarrow\widehat{B}=\widehat{C}=50^o\)
Ta có: \(\widehat{A}+\widehat{B}+\widehat{C}=180^o\)
\(\widehat{A}+100^o=180^o\)
\(\Rightarrow\widehat{A}=80^o\)
50 độ C B A
c,
Theo đề ra: Tam giác ABC cân tại A
\(\Rightarrow\widehat{C}=\widehat{B}=60^o\)
Ta có: \(\widehat{A}+\widehat{B}+\widehat{C}=180^o\)
\(\widehat{A}+120^o=180^o\)
\(\Rightarrow\widehat{A}=60^o\)
C A B 60 độ

a: góc ABC=góc ACB=(180-50)/2=65 độ
b: Xét ΔAMB và ΔANC có
AM=AN
góc BAM chung
AB=AC
=>ΔAMB=ΔANC

a, Vì △ABC cân tại A => \(\widehat{B}=\widehat{C}=\frac{180^o-\widehat{A}}{2}=\frac{180^o-40^o}{2}=\frac{140^o}{2}=70^o\)
b, Vì △ABC cân tại A => \(\widehat{B}=\widehat{C}=50^o\)
Xét △ABC có: \(\widehat{B}+\widehat{C}+\widehat{A}=180^o\)(tổng 3 góc trong tam giác)
\(\Rightarrow50^o+50^o+\widehat{A}=180^o\)\(\Rightarrow\widehat{A}=80^o\)
c, Vì △ABC cân tại A => \(\widehat{B}=\widehat{C}=60^o\)
Xét △ABC có: \(\widehat{B}+\widehat{C}+\widehat{A}=180^o\)(tổng 3 góc trong tam giác)
\(\Rightarrow60^o+60^o+\widehat{A}=180^o\)\(\Rightarrow\widehat{A}=60^o\)

b: \(\widehat{ACE}+\widehat{ACB}=90^0\)
mà \(\widehat{CAE}=180^0-90^0-\widehat{C}=90^0-\widehat{ACB}\)
nên \(\widehat{CAE}=\widehat{ACE}\)
hay ΔAEC cân tại E
a: \(\widehat{A}+\widehat{C}=180^0-30^0=150^0\)
\(\Leftrightarrow2\cdot\widehat{C}+90^0=150^0\)
\(\Leftrightarrow\widehat{C}=30^0\)
\(\Leftrightarrow\widehat{A}=120^0\)

cân tại A => goc C = goc B = 38 độ
góc A = 180 - goc C - góc B = 180 - 38 - 38 = 104 độ
Chúc ban hoc tot!

A B C O K H
a ) Vì \(\Delta ABC\) cân tại A (gt)
\(\Rightarrow\widehat{B}=\widehat{C}=50^o\)
Ta có : \(\widehat{A}=180^o-\left(\widehat{B}+\widehat{C}\right)=180^o-\left(50^o+50^o\right)=180^o-100^o=80^o\)
b ) Xét \(\Delta KBC\) và \(\Delta HCB\) có :
\(\widehat{BKC}=\widehat{CHB}=90^o\)
BC là cạnh chung
\(\widehat{C}=\widehat{B}\left(cmt\right)\)
\(\Rightarrow\Delta KBC=\Delta HCB\) ( cạnh huyền - góc nhọn )
\(\Rightarrow KC=BH\)
C ) Vì \(\Delta KBC=\Delta HCB\left(cmt\right)\)
\(\Rightarrow\widehat{BCK}=\widehat{CBH}\)
\(\Rightarrow\Delta OBC\) cân tại O ( đpcm)
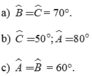

Cân
=>2 góc dáy=nhau
tổng 2 góc đáy=180-40=140 độ
=>mỗi đáy là 140/2=70 độ nhé
Ta có: \(\widehat{A} \) + \(\widehat{B}\) + \(\widehat{C}\) = 1800 (Tổng 3 góc của tam giác)
\(\Rightarrow\) \(\widehat{A} \) + \(\widehat{B}\) = 1800 - \(\widehat{C}\)
\(\Rightarrow\) \(\widehat{A} \) + \(\widehat{B}\) = 1800 - 400 = 1400
Mà: \(\widehat{A} \) = \(\widehat{B}\) (ΔABC cân tại C)
\(\Rightarrow\) \(\widehat{A} \) = \(\widehat{B}\) = \(\dfrac{140^0}{2}\) = 700
Vậy: \(\widehat{A}\) = \(\widehat{B}\) = 700
HT.