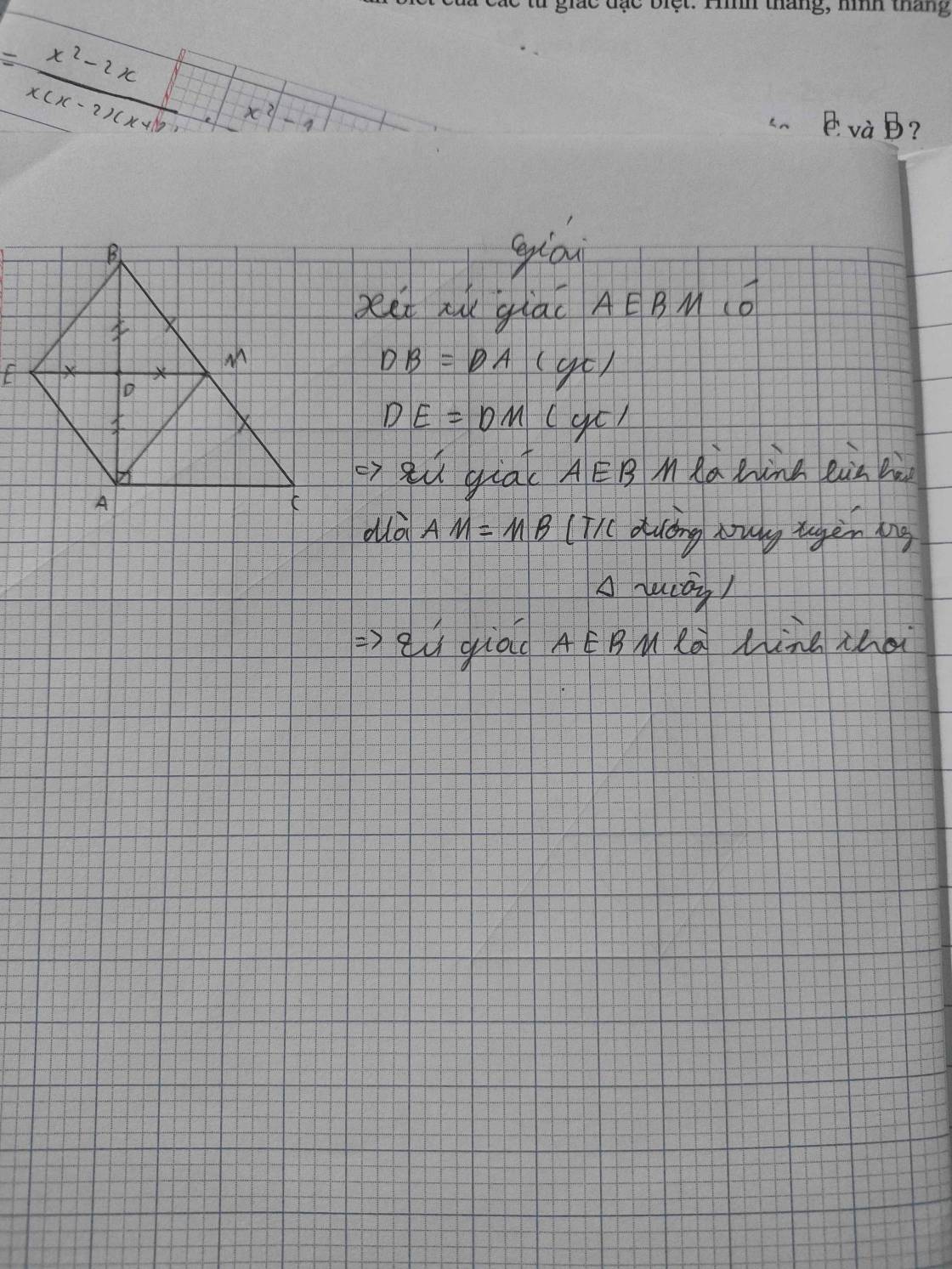Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Xét ΔBMC và ΔDMA có
MB=MD
góc BMC=góc DMA
MC=MA
=>ΔBMC=ΔDMA
=>góc MBC=góc MDA
=>BC//AD
b: Xét tứ giác ABCD có
M là trung điểm chung của AC và BD
=>ABCD là hbh
=>AB=CD
=>CD=CA
=>ΔCAD cân tại C
c: Xét ΔEBD có
EM là trung tuyến
EC=2/3EM
=>C là trọng tâm
=>DC đi qua trung điểm của BE

Ta có \(\left\{{}\begin{matrix}MA=MC\\MB=MD\end{matrix}\right.\Rightarrow ADEB\) là hình bình hành
\(\Rightarrow AD//BC\Leftrightarrow AD//BE\left(1\right)\)
Do ADEB là hình bình hành nên \(AD=BC=CE\) và \(AD//CE\Rightarrow\) ADCE là hình bình hành
\(\Rightarrow\widehat{E}=\widehat{ACB}=\widehat{ABC}\left(2\right)\)
Từ \(\left(1\right);\left(2\right)\Rightarrow\) đpcm

a: Xét ΔABD và ΔACE có
AB=AC
góc ABD=góc ACE
BD=CE
=>ΔABD=ΔACE
=>AD=AE
=>ΔADE cân tại A
b: Xét ΔAHB vuông tại H và ΔAKC vuông tại K có
AB=AC
góc HAB=góc KAC
=>ΔAHB=ΔAKC
=>AH=AK
Xét ΔADE có AH/AD=AK/AE
nên HK//DE
c:
góc HBD+góc D=90 độ
góc KCE+góc E=90 độ
mà góc D=góc E
nên góc HBD=góc KCE
góc MBC=góc HBD
góc MCB=góc KCE
mà góc HBD=góc KCE
nên góc MBC=góc MCB
=>ΔMBC cân tại M

DM và DE là hai tia đối nhau
=>D nằm giữa M và E
mà DM=DE
nên D là trung điểm của ME
Ta có: ΔABC vuông tại A
mà AM là đường trung tuyến
nên MA=MB=MC
Xét tứ giác AMBE có
D là trung điểm chung của AB và ME
=>AMBE là hình bình hành
Hình bình hành AMBE có MA=MB
nên AMBE là hình thoi