Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Xét ΔABD và ΔACE có
AB=AC
\(\widehat{ABD}=\widehat{ACE}\)
BD=CE
Do đó: ΔABD=ΔACE
Suy ra: AD=AE
Xét ΔBHD vuông tại H và ΔCKE vuông tại K cso
BD=CE
\(\widehat{D}=\widehat{E}\)
Do đó: ΔBHD=ΔCKE
Suy ra: BH=CK
b: Xét ΔABH vuông tại H và ΔACK vuông tại K có
AB=AC
BH=CK
Do đó: ΔABH=ΔACK

a: Xét ΔABD và ΔACE có
AB=AC
\(\widehat{ABD}=\widehat{ACE}\)
BD=CE
Do đó: ΔABD=ΔACE
Suy ra: AD=AE và \(\widehat{D}=\widehat{E}\)
Xét ΔHBD vuông tại H và ΔKEC vuông tại K có
BD=CE
\(\widehat{D}=\widehat{E}\)
Do đó: ΔHBD=ΔKCE
Suy ra: BH=CK
b: Xét ΔABH vuông tại H và ΔACK vuông tại K có
AB=AC
\(\widehat{HAB}=\widehat{KAC}\)
Do dó: ΔABH=ΔACK

a) vì tam giác ABC cân tại A nên góc ABC= góc ACB
mà góc ABC = góc HBD ( 2 góc đối đỉnh); góc ACB= góc KCE ( 2 góc đối đỉnh)
=> góc HBD= góc KCE
Xét tam giác HBD và tam giác KCE có :
góc DHB= góc EKC(= 90 độ)
BD=CE (gt)
góc HBD= góc KCE (cmt)
=>tam giác HBD = tam giác KCE (cạnh huyền, góc nhọn)
=>HB=KC( 2 cạnh tương ứng)
b)AHB=AKC ??? chưa rõ
mình cứ xét tam giác AHB và tam giác AKC, nếu là góc bạn tự suy ra thêm 1 bước nhé^^
vì tam giác ABC cân tại A nên góc ABC= góc ACB
mà góc ABC+ góc ABH= góc ACB+ góc ACK=180 độ ( 2 góc kề bù)
=>góc ABH=góc ACK
Xét tam giác AHB và tam giác AKC có:
AB=AC (tam giác ABC cân tại A)
góc ABH=góc ACK( Cmt)
HB=KC( Cmt)

a: Xét ΔABD và ΔACE có
AB=AC
góc ABD=góc ACE
BD=CE
=>ΔABD=ΔACE
=>AD=AE
Xét ΔBHD vuông tại H và ΔCKE vuông tại K có
BD=CE
góc D=góc E
=>ΔBHD=ΔCKE
=>BH=CK
Xét ΔAHB vuông tại H và ΔAKC vuông tại K có
AB=AC
BH=CK
=>ΔAHB=ΔAKC
b: góc IBC=góc HBD
góc ICB=góc KCE
mà góc HBD=góc KCE
nên góc IBC=góc ICB
=>IB=IC
IB+BH=IH
IC+CK=IK
mà IB=IC; BH=CK
nên IK=IH
Xét ΔAHI vuông tại H và ΔAKI vuông tại K có
AH=AK
AI chung
=>ΔAHI=ΔAKI
=>góc HAI=góc KAI
=>AI là phân giác của góc DAE
c: Xet ΔADE có AH/AD=AK/AE
nên HK//DE

a: Xét ΔABD và ΔACE có
AB=AC
\(\widehat{ABD}=\widehat{ACE}\)
BD=CE
DO đó: ΔABD=ΔACE
Suy ra: AD=AE
Xét ΔBHD vuông tại H và ΔCKE vuông tại K có
BD=CE
\(\widehat{D}=\widehat{E}\)
Do đó: ΔBHD=ΔCKE
Suy ra: BH=CK
b: Xét ΔABH vuông tại H và ΔACK vuông tại K có
AB=AC
BH=CK
Do đó: ΔABH=ΔACK

a) Ta có: góc ABC + góc ABD= 180o (kề bù)
góc ACB + góc ACE = 180o (kề bù)
mà góc ABC = góc ACB (tam giác ABC cân tại A)
=> góc ACE = góc ABD
Xét tam giác ABD và ACE có:
AB = AC (tam giác ABC cân tại A)
Góc ACE = góc ABD (cmt)
DB=CE (gt)
=> Tam giác ABD = tam giác ACE (c.g.c)
=> góc BAD = góc CAE (2 góc tương ứng)
Xét 2 tam giác vuông ABH và ACK có:
AB = AC (tam giác ABC cân tại A)
góc BAD = góc CAE (cmt)
=> Tam giác ABH = tam giác ACK (cạnh huyền - góc nhọn)
=>BH = CK (2 cạnh tương ứng)

A B C D E H K
a) Vì \(\Delta ABC\) cân tại A
=> \(\widehat{B}=\widehat{C}\)
mà \(\widehat{ABD}+\widehat{ABC}=180^0\) (kề bù)
và \(\widehat{ACB}+\widehat{ACE}=180^0\) (kề bù)
Do đó: \(\widehat{ABD}=\widehat{ACE}\)
Xét \(\Delta ABC\) và \(\Delta ACE\) có:
AB = AC (gt)
\(\widehat{ABD}=\widehat{ACE}\) (cmt)
DB = CE (gt)
Do đó: \(\Delta ABD=\Delta ACE\left(c-g-c\right)\)
=> \(\widehat{D}=\widehat{E}\) ( hai góc tương ứng)
Xét \(\Delta DBH\) và \(\Delta ECK\) có:
\(\widehat{DHB}=\widehat{CKE}\) ( = 900)
DB = CE (gt)
\(\widehat{D}=\widehat{E}\)(cmt)
Do đó: \(\Delta DBH=\Delta ECK\) (ch -gn)
=> BH = CK (hai cạnh tương ứng)
b) Xét \(\Delta ABH\) và \(\Delta ACK\) có:
CK = BH ( cmt )
\(\widehat{AHB}=\widehat{AKC}\left(=90^0\right)\)
AB = AC (gt)
Do đó: \(\Delta ABH=\Delta ACK\) ( cạnh huyền - cạnh góc vuông)
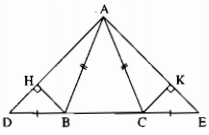
a) Vì ∆ABC cân tại A nên góc ABC =góc ACB (tính chất tam giác cân)
Ta có: góc ABC + góc ABD=180o (hai góc kề bù)
góc ACB + góc ACE=180o (hai góc kề bù)
Suy ra: góc ABD = góc ACE
Xét ∆ABD và ∆ACE, ta có:
AB = AC (gt)
góc ABD = góc ACE (chứng minh trên)
BD = CE (gt)
Suy ra: ∆ABD = ∆ACE (c.g.c)
⇒ góc D = góc E (hai góc tương ứng)
Xét hai tam giác vuông BHD và CKE, ta có:
góc BHD =góc CKE=90o
BD = CE (gt)
góc D = gócE (chứng minh trên)
Suy ra: ∆BHD = ∆CKE (cạnh huyền, góc nhọn)
Suy ra: BH = CK (hai cạnh tương ứng)
Xét tam giác vuông AHB và ACK, ta có:
góc AHB = gócAKC = 90o
AB = AC (gt)
BH = CK (chứng minh trên)
Suy ra: ∆ABH = ∆ACK (cạnh huyền, cạnh góc vuông)
a: Xét ΔABD và ΔACE có
AB=AC
góc ABD=góc ACE
BD=CE
=>ΔABD=ΔACE
=>AD=AE
Xét ΔBHD vuông tại H và ΔCKE vuông tại K có
BD=CE
góc D=góc E
=>ΔBHD=ΔCKE
=>BH=CK
b: Xét ΔAHB vuông tại H và ΔAKC vuông tại K có
AB=AC
BH=CK
=>ΔAHB=ΔAKC