Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Vì tam giác ABC cân tại A có E là trung điểm BC
\(\Rightarrow AE\bot BC\Rightarrow\angle AEB=90\)
\(\Rightarrow\angle AEB=\angle ADB=90\Rightarrow ADEB\) nội tiếp
b) Vì \(\angle HDC=90\Rightarrow\left(HDC\right)\) là đường tròn đường kính HC
\(\Rightarrow\) tâm I của (HDC) là trung điểm HC
c) Ta có: \(\angle HEC+\angle HDC=90+90=180\Rightarrow HDCE\) nội tiếp
\(\Rightarrow\left(I\right)\) đi qua điểm E và D
Vì ADEB nội tiếp \(\Rightarrow\left(O\right)\) đi qua điểm E và D
\(\Rightarrow\) 2 điểm chung là D và E
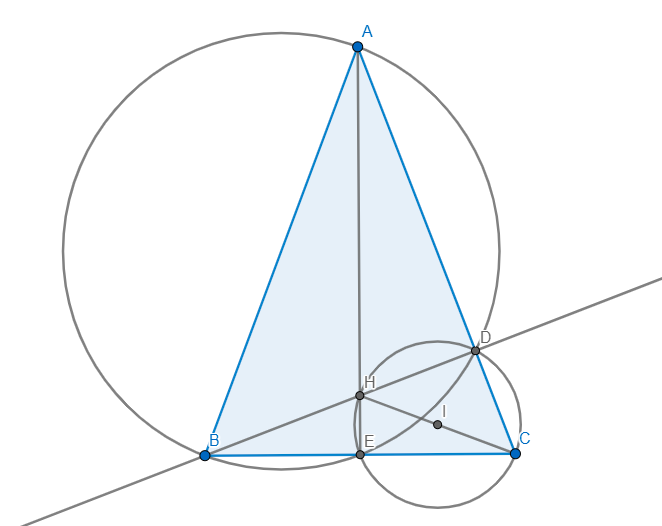

a) Ta có: ΔABC cân tại A(gt)
mà AE là đường trung tuyến ứng với cạnh BC(gt)
nên AE là đường cao ứng với cạnh BC(Định lí tam giác cân)
Xét tứ giác ABED có
\(\widehat{AEB}=\widehat{ADB}\left(=90^0\right)\)
nên ABED là tứ giác nội tiếp(Dấu hiệu nhận biết tứ giác nội tiếp)
hay A,B,E,D cùng thuộc (O)
b) Xét tứ giác HDCE có
\(\widehat{HEC}+\widehat{HDC}=180^0\)
nên HDCE là tứ giác nội tiếp(Dấu hiệu nhận biết tứ giác nội tiếp)
Tâm I của đường tròn ngoại tiếp tứ giác HDCE là trung điểm của HC

1) Xét (O) có
ΔDAB nội tiếp đường tròn (O)(Vì D,A,B∈(O))
mà AB là đường kính của (O)(gt)
nên ΔDAB vuông tại D(Định lí)
⇒BD⊥AD tại D
hay BD⊥AC
Xét (O) có
ΔEAB nội tiếp đường tròn(E,A,B∈(O))
mà AB là đường kính(gt)
nên ΔEAB vuông tại E(Định lí)
⇒AE⊥EB tại E
hay AE⊥BC tại E
Xét ΔCAB có
BD là đường cao ứng với cạnh AC(cmt)
AE là đường cao ứng với cạnh BC(cmt)
BD\(\cap\)AE={H}
Do đó: H là trực tâm của ΔCAB(Tính chất ba đường cao của tam giác)
⇔CH là đường cao ứng với cạnh AB
hay CH⊥AB(đpcm)

a, Gọi O là trung điểm của AH thì OE = OA = OH = OD
b, HS tự làm
a. Gọi O là trung điểm AB
Tam giác ADB vuông tại D
=> Tam giác ADB nội tiếp đường tròn tâm O, đường kính AB (1)
Tam giác ABC cân tại A có AE là trung tuyến
=> AE cũng là đường cao của tam giác
=>AE vuông góc BC
Tam giác AEB vuông tại E
=>Tam giác AEB nội tiếp đường tròn tâm O, đường kính AB (2)
(1)(2) => A,D,B,E cùng thuộc đường tròn tâm O, đường kính AB
b. Tam giác HCD vuông tại D
=>Tam giác HCD nội tiếp đường tròn đường kính HC
=>Tâm O' của đường tròn đi qua 3 điểm H,C,D là trung điểm của cạnh HC.