Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

A B C M D E K
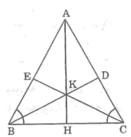
Các đường phân giác BD và CE cắt nhau tại K nên AK la đường phân giác của góc A.
Trong một tam giác cân, đường phân giác xuất phát từ đỉnh đồng thời là đường trung tuyến, do đó AK đi qua trung điểm M của BC.

Các đường phân giác BD và CE cắt nhau tại K nên AK là đường phân giác của góc A.
Gọi H là trung điểm của BC
Trong tam giác cân đường phân giác xuất phát từ đỉnh đối diện với đáy đồng thời là đường trung tuyến ứng với cạnh đáy.
Vậy AK đi qua trung điểm H của BC.

Hướng dẫn :Trong 1 tam giác cân thì phân giác đồng thời là trung điểm của cạnh đối diện
Xét \(\Delta\)ABC có 2 đường phân giác là BD và CE cắt nhau tại K
=>AK là đường phân giác của góc BAC
Do: \(\Delta\)ABC cân tại A
Nên:AK đồng thời là đường trung tuyến
Vậy AK đi qua trung tuyến BC

JUNPHAM2018 đúng rồi !!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!