Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Vận dụng đinh lý 1 về đường trung bình của tam giác suy ra APMQ là hình thoi do có 4 cạnh bằng nhau.
b) Vì PQ ^ AM mà AM ^ BC (tính chất tamgiacs cân) nên PQ//BC.
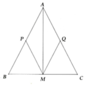

a: ΔABC cân tại A
mà AM là đường trung tuyến
nên AM là đường cao và AM là phân giác của \(\widehat{BAC}\)
Xét tứ giác APMQ có
AP//MQ
AQ//MP
Do đó: APMQ là hình bình hành
Hình bình hành APMQ có AM là phân giác của góc PAQ
nên APMQ là hình thoi
b: Xét ΔABC có
M là trung điểm của BC
MP//AC
Do đó: P là trung điểm của AB
Xét ΔABC có
M là trung điểm của BC
MQ//AB
Do đó: Q là trung điểm của AC
Xét ΔABC có
P,Q lần lượt là trung điểm của AB,AC
=>PQ là đường trung bình của ΔABC
=>PQ//BC
c: Xét ΔABC có M,Q lần lượt là trung điểm của CB,CA
=>MQ là đường trung bình của ΔABC
=>MQ//AB và \(MQ=\dfrac{AB}{2}\)
mà \(MQ=\dfrac{MD}{2}\)
nên MD=AB
MQ//AB
=>MD//AB
Xét tứ giác ABMD có
AB//MD
AB=MD
Do đó: ABMD là hình bình hành
d: Xét tứ giác AMCD có
Q là trung điểm chung của AC và MD
Do đó: AMCD là hình bình hành
Hình bình hành AMCD có \(\widehat{AMC}=90^0\)
nên AMCD là hình chữ nhật
Hình chữ nhật AMCD muốn trở thành hình vuông thì CA là phân giác của góc MCD
=>\(\widehat{ACB}=\dfrac{1}{2}\cdot90^0=45^0\)

Mình không biết vẽ hình trên đây bạn tự vẽ hình nhé
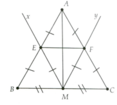
Xét tam giác BAC có: BM=CM(M là trung điểm của BC)
ME//AC(Mx//AC)
=>AE=BE(hay E là trung điểm của AB)
Xét tam giác CBA có: BM=CM(M là trung điểm của BC)
MF//AB(My//AB)
=>AF=CF(hay F là trung điểm của AC)
Xét tam giác ABC có: AE=BE
AF=CF
=>EF là đường trung bình của tam giác ABC
b, Xét tứ giác AEMF có: ME//AF(Mx//AC)
MF//AE(My//AB)
=>AEMF là hình bình hành
Ta có: AE=BE; AF=CF
mà AB=AC(tam giác ABC cân tại A)
=>AE=BE=AF=CF
Xét hình bình hành AEMF có:AF=AE
=>AEMF là hình thoi
=> AM vuông góc với EF và AM đi qua trung điểm của EF
=>AM là đường trung trực của EF

Cm: a) Ta có: BA ⊥⊥AC (gt)
HD // AB (gt)
=> HD ⊥⊥AC => ˆHDA=900HDA^=900
Ta lại có: AC ⊥⊥AB (gt)
HE // AC (gt)
=> HE ⊥⊥AB => ˆHEA=900HEA^=900
Xét tứ giác AEHD có: ˆA=ˆAEH=ˆHDA=900A^=AEH^=HDA^=900
=> AEHD là HCN => AH = DE
b) Gọi O là giao điểm của AH và DE
Ta có: AEHD là HCN => OE = OH = OD = OA
=> t/giác OAD cân tại O => ˆOAD=ˆODAOAD^=ODA^ (1)
Xét t/giác ABC vuông tại A có AM là đường trung tuyến
-> AM = BM = MC = 1/2 BC
=> t/giác AMC cân tại M => ˆMAC=ˆCMAC^=C^
Ta có: ˆB+ˆC=900B^+C^=900 (phụ nhau)
ˆC+ˆHAC=900C^+HAC^=900 (phụ nhau)
=> ˆB=ˆHACB^=HAC^ hay ˆB=ˆOADB^=OAD^ (2)
Từ (1) và (2) => ˆODA=ˆBODA^=B^
Gọi I là giao điểm của MA và ED
Xét t/giác IAD có: ˆIAD+ˆIDA+ˆAID=1800IAD^+IDA^+AID^=1800 (tổng 3 góc của 1 t/giác)
=> ˆAID=1800−(IAD+ˆIDA)AID^=1800−(IAD+IDA^)
hay ˆAID=1800−(ˆB+ˆC)=1800−900=900AID^=1800−(B^+C^)=1800−900=900
=> AM⊥DEAM⊥DE(Đpcm)
c) (thiếu đề)

a: BC=15cm
=>AM=7,5cm
b: Xét tứ giác AEMF có góc AEM=góc AFM=góc FAE=90 độ
nên AEMF là hình chữ nhật

a) Mx đi qua trung điểm M của BC và song song với AC. Suy ra Mx đi qua trung điểm E của AB (theo Định lí 1).
Tương tự, ta được F cũng là trung điểm của AC. Khi đó EF trở thành đường trung bình của tam giác ABC;
b) Do ME và MF cũng là đường trung bình nên có ME = MF = AE = AF. Suy ra AM là đường trung trực của EF.