Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Bạn tự vẽ hình nha!
a.
Xét tam giác ABM và tam giác ACM có:
AB = AC (tam giác ABC cân tại A)
B = C (tam giác ABC cân tại A)
BM = CM (AM là trung tuyến của tam giác ABC)
=> Tam giác ABM = Tam giác ACM (c.g.c)
b.
Tam giác ABM = Tam giác ACM (theo câu a)
=> M1 = M2 (2 góc tương ứng)
mà M1 + M2 = 180 (2 góc kề bù)
=> M1 = M2 = 180/2 = 90
=> AM _I_ BC
( Cái này bạn chứng minh theo cách: AM là trung tuyến của tam giác ABC cân tại A nên AM là đường trung trực của tam giác ABC cũng được. Tại mình sợ bạn chưa học tới)
BM = CM = BC/2 (AM là trung tuyến của tam giác ABC)
=> BM = CM = 10/2 = 5
Áp dụng định lí Pytago vào tam giác ABM vuông tại A ta có:
AB^2 = BM^2 + AM^2
13^2 = 5^2 + AM^2
AM^2 = 169 - 25
AM = 12
Ta có: AG = 2/3 AM (tính chất trọng tâm)
=> AG = 2/3 . 12
AG = 8

tham khảo
+ Vì MAM là đường trung tuyến của ΔABC(gt)ΔABC(gt)
=> MM là trung điểm của BC.BC.
=> BM=CM=12BCBM=CM=12BC (tính chất trung điểm).
=> BM=CM=12.16=162=8(cm).BM=CM=12.16=162=8(cm).
+ Xét ΔABCΔABC có:
AB=AC=17cm(gt)AB=AC=17cm(gt)
=> ΔABCΔABC cân tại A.A.
Có AMAM là đường trung tuyến (gt).
=> AMAM đồng thời là đường cao của ΔABC.ΔABC.
=> AM⊥BC.AM⊥BC.
+ Xét ΔABMΔABM vuông tại M(cmt)M(cmt) có:
AM2+BM2=AB2AM2+BM2=AB2 (định lí Py - ta - go).
=> AM2+82=172AM2+82=172
=> AM2=172−82AM2=172−82
=> AM2=289−64AM2=289−64
=> AM2=225AM2=225
=> AM=15(cm)AM=15(cm) (vì AM>0AM>0).
+ Vì G là trọng tâm của ΔABC(gt).ΔABC(gt).
=> AG=23AMAG=23AM (tính chất trọng tâm của tam giác).
=> AG=23.15AG=23.15
=> AG=303AG=303
=> AG=10(cm).AG=10(cm).
Vậy AM=15(cm);AG=10(cm).

a)tam giác abc vuông tại a nên theo định lí Py-ta-go,ta có :
BC2 =AC2+AB2
hay BC^2 =12^2+9^2
BC^2=81+144=225
BC=15CM
b) tam giác abc vuông tại a có đường trung tuyến ứng với cạnh huyền bc
=> AM=1/2 BC
hay AM=1/2.15
AM=7.5 cm
ta có g là trọng tâm cura tam giác abc
=> GM=1/3 AM ( tính chất đường trung tuyến )
GM=1/3.7,5
GM=2,5 cm

A B C M 1 2 Q G
A) XÉT \(\Delta ABM\)VÀ\(\Delta ACM\)CÓ
\(AB=AC\left(GT\right)\)
\(\widehat{A_1}=\widehat{A_2}\left(GT\right)\)
AM LÀ CẠNH CHUNG
=>\(\Delta ABM\)=\(\Delta ACM\)( C-G-C)
TRONG TAM GIÁC CÂN TIA PHÂN GIÁC CŨNG LÀ ĐƯỜNG CAO
=> AM LÀ ĐƯỜNG CAO CỦA \(\Delta ABC\)
\(\Rightarrow AM\perp BC\)
B) TRONG TAM GIÁC CÂN TIA PHÂN GIÁC CŨNG LÀ TRUNG TUYẾN
=> AM LÀ TRUNG TUYẾN THỨ NHẤT CỦA \(\Delta ABC\)
MÀ BG LÀ ĐƯỜNG TRUNG TUYẾN THỨ HAI CỦA \(\Delta ABC\)
HAI ĐƯỜNG TRUNG TUYẾN NÀY CẮT NHAU TẠI G
\(\Rightarrow G\)LÀ TRỌNG TÂM CỦA \(\Delta ABC\)

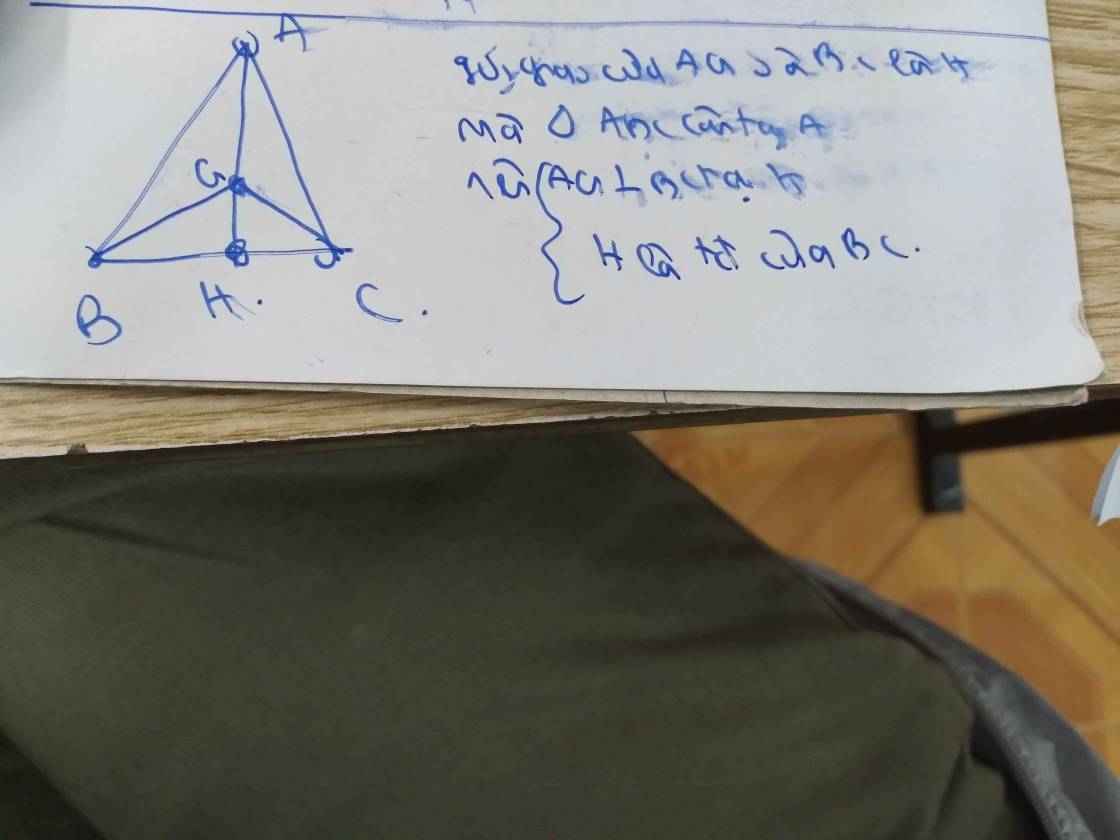
Vì AH là đường Phân giác của \(\Delta ABC\)cân tại A
\(\Rightarrow\)AH là đường cao cửa tam giác cân ABC
\(\Rightarrow AH\perp BC\equiv H\)\(\Rightarrow\Delta AHB\)vuuoong tại H
Ta có Đường phân giác AH đi qua trọng tâm G
\(\Rightarrow\)AH là trung tuyến của \(\Delta ABC\) đi qua BC
\(\Rightarrow\)HB=HC
Mà HB+HC=BC
\(\Rightarrow\)\(HB=HC=\frac{BC}{2}\)\(=\frac{16}{2}=4\)
Ta có: \(AB^2=AH^2+HB^2\)(áp dụng định lý pyta go cho tam giác AHB vuông tại H)
\(\Rightarrow10^2=AH^2+4^2\)
\(\Rightarrow AH^2=10^2-4^2\)\(=84\)
\(\Rightarrow\sqrt{84}\)
Mà G là trọng tâm của tam giác ABC
\(\Rightarrow AG=\frac{2}{3}AH\)
còn lại tự tính nha ta hướng dẫn là rồi đó
có một số chỗ ta nhầm bỏ từ chỗ \(HB=HC=\frac{BC}{2}=\frac{16}{2}\)\(=4\)
sửa lại :\(HB=HC=\frac{BC}{2}=\frac{16}{2}\)\(=8\)
\(AB^2=AH^2+HB^2\)(áp dụng định lý pytago cho \(\Delta AHB\)vuông tại A)
\(\Rightarrow10^2=AH^2+8^2\)
\(\Rightarrow AH^2=10^2-8^2=36\)
\(\Rightarrow AH=6\)
Mà G là trọng tâm của \(\Delta ABC\)
\(\Rightarrow AG=\frac{2}{3}AH\)
hay \(AG=\frac{2}{3}.6\)
\(\Rightarrow AG=4cm\)
vậy AG=4cm