Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Xét ΔACD có \(\widehat{ACD}\) là góc tù
nên AD là cạnh lớn nhất
Suy ra: AD>AC
hay AD>AB

Xét △ BCF và △ CBE có:
\(\widehat{B}=\widehat{C}\) ( △ ABC cân tại A )
BC chung
\(\widehat{E}=\widehat{F}\left(=90^0\right)\)
⇒ △ BCF = △ CBE
⇒ BE = CF ( 2 cạnh tương ứng ) (1)
Có \(\widehat{DCF}>90^0\) ⇒ DF > CF (2)
Từ (1) và (2) ⇒ DF > BE

Bài 1: A B C D x
Cm: Do Bx nằm giữa tia BA và BC nên \(\widehat{ABx}+\widehat{xBC}=\widehat{B}\)
=> \(\widehat{xBC}< \widehat{B}\) hay \(\widehat{DBC}< \widehat{B}\)(1)
D là điểm nằm ngoài t/giác ABC => tia CA nằm giữa CB và CD
=> \(\widehat{BCA}+\widehat{ACD}=\widehat{BCD}\)
=> \(\widehat{BCA}< \widehat{BCD}\) (2)
Mà \(\widehat{B}=\widehat{BCA}\) (Vì t/giác ABC cân tại A) (3)
Từ (1); (2); (3) => \(\widehat{DBC}< \widehat{BCD}\)
=> DC < BD (quan hệ giữa cạnh và góc đối diện)

a)
+ Trong ΔABC có: góc ABC đối diện cạnh AC, góc ACB đối diện cạnh AB.
b) ΔAED có:
⇒ AE < AD hay AD > AE

a.
b. Xét ΔADE có góc ADE < góc AED (chứng minh ở phần a)
=> AE < AD (Quan hệ giữa góc - cạnh đối diện trong tam giác)
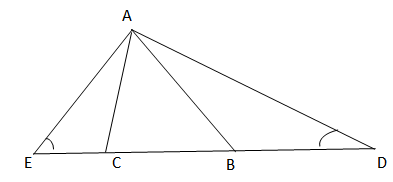
a) So sánh ˆADCADC^ và ˆAECAEC^
Ta có: AC < AB
=> ˆABC<ˆACBABC^<ACB^ (1)
Vì AC = EC => ∆AEC cân tại C
=> ˆAEC<ˆCAEAEC^<CAE^
Mà ˆACB=ˆAEC+ˆEACACB^=AEC^+EAC^ (góc ngoài tại C của ∆AEC)
=> ˆACB=2.ˆAECACB^=2.AEC^ (2)
Chứng minh tương tự : ˆABC=2ˆADCABC^=2ADC^ (3)
Từ (1), (2), (3) => 2ˆAEC=2ˆADC2AEC^=2ADC^ hay ˆAEC=ˆADCAEC^=ADC^
b) ∆AED có:
ˆAED=ˆADEAED^=ADE^ (chứng minh trên) => AD = AE
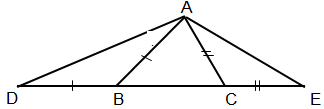

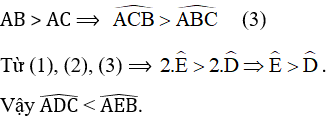



a) Vì trong một tam giác cân hai góc ở đáy không bao giờ là hai góc tù
nên \(\widehat{ACB}=\widehat{ABC}< 90^0\)
Ta có: \(\widehat{ACB}+\widehat{ACD}=180^0\)(hai góc kề bù)
mà \(\widehat{ACB}< 90^0\)(cmt)
nên \(\widehat{ACD}>90^0\)
Xét ΔACD có \(\widehat{ACD}\) tù(cmt)
mà cạnh đối diện với góc ACD là AD
nên AD là cạnh lớn nhất trong ΔACD(Trong một tam giác tù, cạnh đối diện với góc tù là cạnh lớn nhất)
hay AD>AC
mà AC=AB(ΔABC cân tại A)
nên AD>AB