Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Xét ΔABN vuông tại A và ΔACM vuông tại A có
AB=AC
góc ABN=góc ACM
=>ΔABN=ΔACM
b: ΔABN vuông tại A có AE là trung tuyến
nên AE=BE=NE=BN/2
ΔACM vuông tại A có AD là trung tuyến
nên AD=CM/2=BN/2=AE
góc EAB=góc EBA=15 độ
góc DAC=góc DCA=15 độ
=>góc EAD=90-15-15=60 độ
Xét ΔAED có AE=AD và góc EAD=60 độ
nên ΔAED đều
c: Xét ΔIBC có góc IBC=góc ICB
nên ΔIBC cân tại I
=>IB=IC
=>I nằm trên trung trực của BC
=>A,I,H thẳng hàng

a) Ta có: AK+KB=AB(K nằm giữa A và B)
AH+HC=AC(H nằm giữa A và C)
mà AK=AH(gt)
và AB=AC(ΔABC cân tại A)
nên KB=HC
Xét ΔKBC và ΔHCB có
KB=HC(cmt)
\(\widehat{KBC}=\widehat{HCB}\)(hai góc ở đáy của ΔABC cân tại A)
BC chung
Do đó: ΔKBC=ΔHCB(c-g-c)
Suy ra: \(\widehat{KCB}=\widehat{HBC}\)(hai góc tương ứng)
hay \(\widehat{OBC}=\widehat{OCB}\)
Xét ΔOBC có \(\widehat{OBC}=\widehat{OCB}\)(cmt)
nên ΔOBC cân tại O(Định lí đảo của tam giác cân)
b) Xét ΔAKH có AK=AH(gt)
nên ΔAKH cân tại A(Định nghĩa tam giác cân)
Ta có: ΔAKH cân tại A(cmt)
nên \(\widehat{AKH}=\dfrac{180^0-\widehat{A}}{2}\)(Số đo của một góc ở đáy trong ΔAKH cân tại A)(1)
Ta có: ΔABC cân tại A(gt)
nên \(\widehat{ABC}=\dfrac{180^0-\widehat{A}}{2}\)(Số đo của một góc ở đáy trong ΔABC cân tại A)(2)
Từ (1) và (2) suy ra \(\widehat{AKH}=\widehat{ABC}\)
mà \(\widehat{AKH}\) và \(\widehat{ABC}\) là hai góc ở vị trí đồng vị
nên KH//BC(Dấu hiệu nhận biết hai đường thẳng song song)

a, Xét tam giác ABE và tam giác ACD
AB = AC
AE = AD
^A _ chung
Vậy tam giác ABE = tam giác ACD (c.g.c)
=> BE = CD ( 2 cạnh tương ứng )
=> ^ABE = ^ACD ( 2 góc tương ứng )
b, Ta có BD = AB - AD ; EC = AC - AE => BD = EC
Xét tam giác KBD và tam giác KCE có
^BKD = ^CKE ( đối đỉnh )
^KBD = ^KCE (cmt)
BD = CE (cmt)
Vậy tam giác KBD = tam giác KCE (g.c.g)
c, Xét tam giác ABH và tam giác ACH có
^B = ^C
AH _ chung
AB = AC
Vậy tam giác ABH = tam giác ACH ( c.g.c )
=> ^BAH = ^CAH ( 2 góc tương ứng )
=> AH là đường phân giác
hay AK là đường phân giác
d, Xét tam giác ABC cân tại A có AK là phân giác đồng thời là đường cao
hay AK vuông BC
e, Ta có AD/AB = AE/AC => DE//BC (Ta lét đảo)

+) Xét ΔABH và ΔACK, ta có:
AB = AC ( vì tam giác ABC cân tại A)
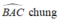
AH = AK (giả thiết)
Suy ra: ΔABH = ΔACK(c.g.c)

+ Do đó, tam giác OBC cân tại O.

a: Xét ΔADC và ΔAEB có
AD=AE
góc DAC chung
AC=AB
=>ΔADC=ΔAEB
b: AD+DB=AB
AE+EC=AC
mà AB=AC và AD=AE
nên DB=EC
Xét ΔDBC và ΔECB có
DB=EC
góc DBC=góc ECB
BC chung
=>ΔDBC=ΔECB
=>góc KBC=góc KCB
=>ΔKBC cân tại K

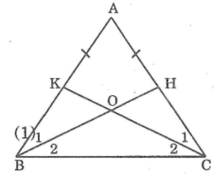
Hình vẽ:
Giải:
Xét \(\Delta ABH\) và \(\Delta ACK\) có:
\(AH=AK\left(gt\right)\)
\(\widehat{A}\) là góc chung
\(AB=AC\) ( Vì \(\Delta ABC\) cân tại \(A\) )
Do đó: \(\Delta ABH=\Delta ACK\left(c.g.c\right)\)
\(\Rightarrow\widehat{B_2}=\widehat{C_2}\) ( cặp góc tương ứng )
Mà \(\widehat{B}=\widehat{C}\) ( Do \(\Delta ABC\) cân tại \(A\) )
\(\Rightarrow\widehat{B}-\widehat{B_2}=\widehat{C}-\widehat{C_2}\)
\(\Rightarrow\widehat{B_1}=\widehat{C_1}\)
\(\Rightarrow\Delta OBC\) cân tại \(O\) . \(\left(đpcm\right)\)



a: Xét ΔAKB và ΔAHC có
AK=AH
góc BAK chung
AB=AC
=>ΔAKB=ΔAHC
=>CH=BK
b: Xét ΔOHB và ΔOKC có
góc OHB=góc OKC
HB=KC
góc OBH=góc OCK
=>ΔOHB=ΔOKC
c: ΔOHB=ΔOKC
=>OB=OC
=>AO là trung trực của BC
=>AO vuông góc BC tại I
=>AB>AI