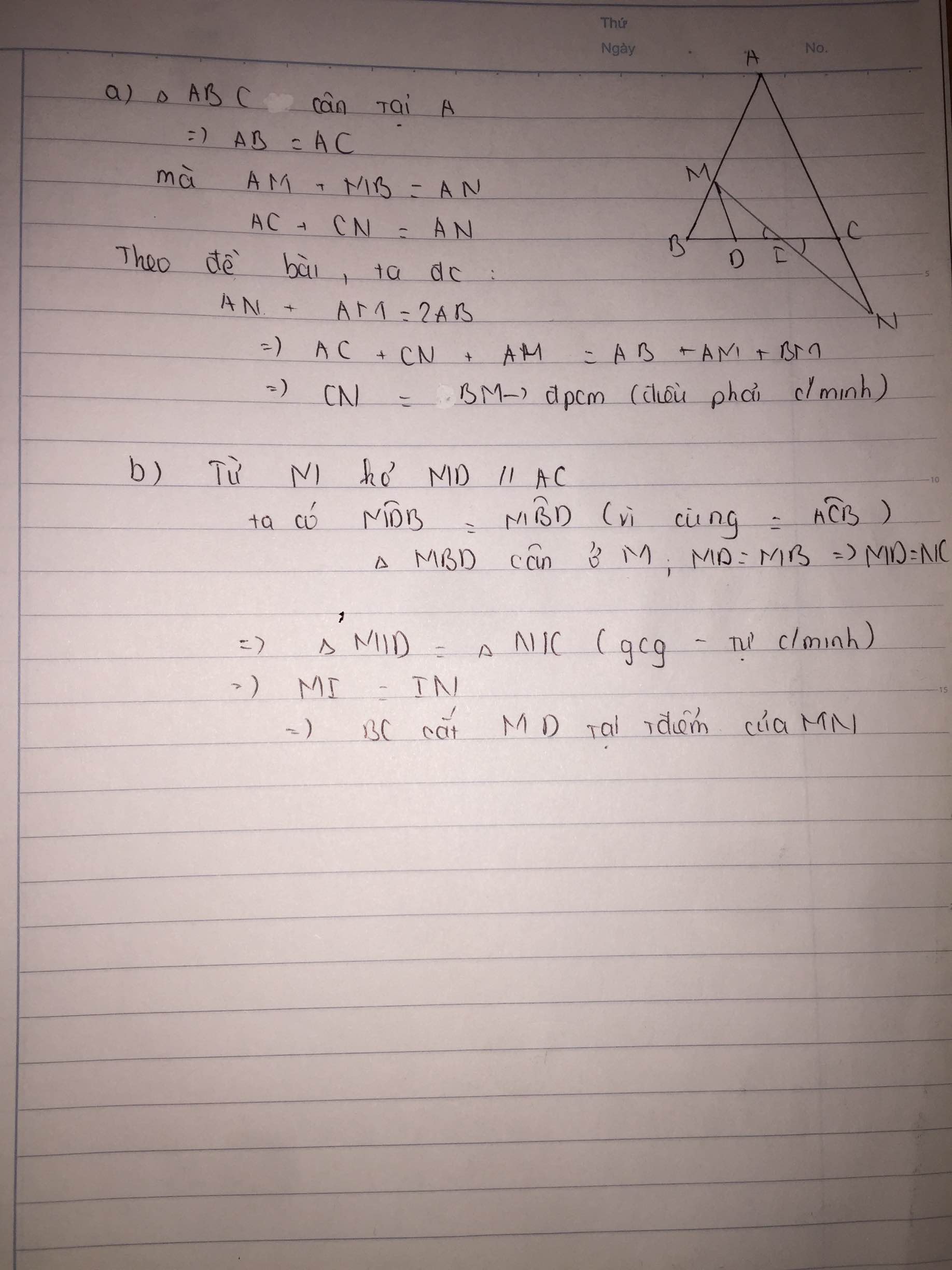Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

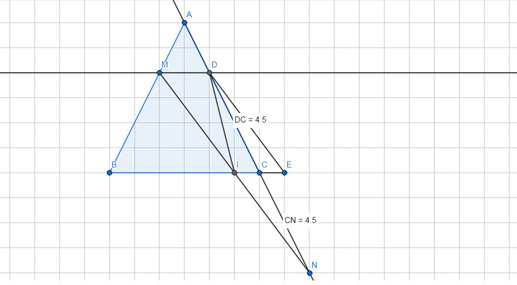
- Kẻ MD//BC (D thuộc AC). Trên tia đối của tia CI lấy điểm E sao cho CI=CE.
- Ta có: Góc ABC=Góc AMD (MD//BC và đồng vị).
Góc ACB=Góc ADM (MD//BC và đồng vị).
Góc ABC=Góc ACB (Tam giác ABC cân tại A).
=>Góc AMD=Góc ADM.
=> Tam giác ADM cân tại A.
=> AD=AM.
*AM+AN=2AB =>AD+AN=2AB =>AD+AN=2AC
Mà AD+DC=AC nên DC+AC=AN=AC+CN =>DC=CN hay C là trung điểm DN.
- Xét tam giác ICN và tam giác ECD có:
IC=CE (gt)
Góc ICN= Góc ECD (đối đỉnh)
DC=CN (cmt)
=> Tam giác ICN= Tam giác ECD (c-g-c).
=> IN=DE (2 cạnh tương ứng).
Góc INC= Góc EDC (2 góc tương ứng) mà 2 góc này ở vị tri so le trong nên DE//IN.
- Xét tam giác MDI và tam giác EID có:
Góc MDI=Góc EID (MD//IE và so le trong).
DI là cạnh chung.
Góc MID= Góc EDI (MI//DE và so le trong).
=> Tam giác MDI= Tam giác EID (g-c-g)
=>MI=DE (2 cạnh tương ứng ) mà IN=DE (cmt) nên MI=IN hay I là trung điểm MN.

a. 2AB = AM + AN
=> 2AB = AM + AC + CN
=> 2AB = AM + AB + CN
=> AB = AM + CN
=> AM + BM = AM + CN
=> BM = CN
b. BC cat MN tai F
ve~ NE // BC ( E thuoc AB keo dai )
suy ra gocABC = gocAEN
gocANE = gocACB
ma gocABC = gocACB ( tam giac ABC can tai A )
=> hinh thang BCNE la hinh thang can
=> CN = BE
ma CN = BM ( cm cau a )
=> BM = BE
BF // NE
=> BF la duong trung binh tam giac MNE => MF = FN

1) dùng 2 góc đồng vị (góc B với M hoặc góc C với N)
2) cm 2 góc BAE và CAE bằng nhau
suy ra tam giác BAE = tam giác CAE
suy ra AB = AC; EB = EC
nên AE là đường trung trực của BC
suy ra AE vuông góc với BC
cm AI vuông gõ với BC suy ra A,I, E thẳng hàng

a) 2AB=AM+AN => AB+AC=AB-BM+AC+CN
=>0= CN-BM => CN=BM.
b)Từ M kẻ đường song song với AN cắt BC tại K.
Ta có: tam giác ABC cân tại Á nên góc B=góc C. Mà MK//AN => góc MKB =góc ABC => góc MKB=góc B=> MB=MK=CN
=> 180độ - góc MKB=180 độ - góc B=> góc MKI=góc ICN
MÀ góc KMN=góc INA (so le trong).
Vậy tam giác MKI bằng tam giác NIC(g.c.g)=>MI=NI
Hình tự vẽ :>
a) Ta có:
AM+AN=2AB
Mà AB=AC (△ABC cân)
\(\Rightarrow\)AM+AN=AB+AC
\(\Rightarrow\)AM+AC+CN=AM+MB+AC
\(\Rightarrow\)AM+AC+CN-AM-MB-AC=0
\(\Rightarrow\)(AM-AM)+(AC-AC)+CN-MB=0
\(\Rightarrow\)CN=MB (đpcm)
b) Kẻ BH là tia đối BI, BH=IC, nối MH
Ta có:
ACI+ICN=180o (kề bù)
ABI+MBH=180o (kề bù)
mà ABI=ACI (△ABC cân)
\(\Rightarrow\)MBH=ICN
Xét △MBH và △NCI có:
BH=CI (cách vẽ)
MBH=NCI (cmt)
MB=CN (c/m câu a)
\(\Rightarrow\) △MBH=△NCI (c.g.c)
\(\Rightarrow\)MHB=CIN (2 góc tương ứng)
\(\Rightarrow\)MH=NI (2 cạnh tương ứng)
Ta có:
CIN=NIB (đối đỉnh)
\(\Rightarrow\)MHB=MIB
\(\Rightarrow\)△MHI cân
\(\Rightarrow\)MH=MI
Mà MH=NI
\(\Rightarrow\)MI=NI
\(\Rightarrow\)MC cắt MN ở trđ I của MN (đpcm)