Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Giải
b)Xét tam giác BAH và CAH có:
AB=AC(gt)
góc B =góc C(gt)
AH chung
\(\Rightarrow\)tam giác BAH =CAH (c.g.c)
\(\Rightarrow\)góc BAH=CAH (2 góc t/ư)
Mặt khác AH nằm giữa AB và AC ,chia góc A thành 2 góc bằng nhau
Mà H là trung điểm BC
\(\Rightarrow\)AH là tia phân giác góc A và vuông góc BC

a: Ta có: ΔAHB vuông tại H
=>\(AH^2+HB^2=AB^2\)
=>\(AH^2=10^2-6^2=64\)
=>\(AH=\sqrt{64}=8\left(cm\right)\)
b: Xét ΔAHB vuông tại H và ΔAHC vuông tại H có
AB=AC
AH chung
Do đó: ΔAHB=ΔAHC
=>\(\widehat{BAH}=\widehat{CAH}\)
=>AH là phân giác của góc BAC
c: Ta có: ΔAHB=ΔAHC
=>BH=CH
Xét ΔBMH vuông tại M và ΔCNH vuông tại N có
BH=CH
\(\widehat{B}=\widehat{C}\)
Do đó: ΔBMH=ΔCNH
d: Xét ΔABO vuông tại B và ΔACO vuông tại C có
AO chung
AB=AC
Do đó: ΔABO=ΔACO
=>OB=OC
=>ΔOBC cân tại O

a: Xét ΔAHB vuông tại H và ΔAHC vuông tại H có
AB=AC
AH chung
Do đó: ΔAHB=ΔAHC
Ta có: ΔABC cân tại A
mà AH là đường cao
nên AH là đường phân giác
b: Xét ΔAMH vuông tại M và ΔANH vuông tại N có
AH chung
\(\widehat{MAH}=\widehat{NAH}\)
DO đó; ΔAMH=ΔANH
Suy ra: AM=AN và HM=HN
=>AH là đường trung trực của MN
hay AH\(\perp\)MN
c, Xét ▲AMK và ▲ANK có:
Góc K1 = K2 ( Ah vuông với Mn)
Ak chung
A1=A2 (cmt)
Sra ▲AMK = ▲ANK ( cgv-gn)
Do đó MK = NK ( 2 cạnh tương ứng)
Xét ▲NMP có:
NH là trung tuyến (do HM=HP)
PK là trung tuyến ( do MK = NK) cmt (1)
Suy ra Q là trọng tâm △NMP (2)
Từ (1) và (2) suy ra P,Q,K thẳng hàng

`#3107.101107`
`a,`
Xét $\triangle ABH$ và $\triangle ACH$:
`AB = AC` $(\triangle ABC$cân tại A`)`
\(\widehat{B}=\widehat{C}\) $(\triangle ABC$cân tại A`)`
`HB = HC ( H` là trung điểm của BC`)`
$=> \triangle ABH = \triangle ACH (c - g - c)$
Vì $\triangle ABH = \triangle ACH$
`=>`\(\widehat{AHB}=\widehat{AHC}\left(\text{2 góc tương ứng}\right)\)
Mà `2` góc này nằm ở vị trí kề bù
`=>` \(\widehat{AHB}+\widehat{AHC}=180^0\)
`=>` \(\widehat{AHB}=\widehat{AHC}=\dfrac{180^0}{2}=90^0\) `=> AH \bot BC`
`b,`
Vì $\triangle ABH = \triangle ACH (a)$
`=>`\(\widehat{BAH}=\widehat{CAH}\left(\text{2 góc tương ứng}\right)\)
Xét $\triangle AHM$ và $\triangle AHN$:
AH chung
\(\widehat{MAH}=\widehat{NAH}\left(CMT\right)\)
\(\widehat{AMH}=\widehat{ANH}\left(=90^0\right)\)
$=> \triangle AHM = \triangle AHN (ch - gn)$
`c,`
Xét $\triangle HMB$ và $\triangle HNC$:
\(\widehat{HMB}=\widehat{HNC}\left(=90^0\right)\)
`HB = HC` `(`gt`)`
\(\widehat{HBM}=\widehat{HCN}\) $(\triangle ABC$ cân tại A`)`
$=> \triangle HMB = \triangle HNC (ch - gn)$
`=>`\(\widehat{BHM}=\widehat{CHN}\left(2\text{ góc tương ứng}\right)\) `(1)`
Vì \(\left\{{}\begin{matrix}\widehat{MHB}+\widehat{KHB}=\widehat{MHK}\\\widehat{NHC}+\widehat{IHC}=\widehat{NHI}\end{matrix}\right.\)
Mà \(\widehat{MHK}=\widehat{NHI}\left(\text{đối đỉnh}\right)\) `(2)`
Từ `(1)` và `(2)` `=>` \(\widehat{KHB}=\widehat{IHC}\)
Xét $\triangle KHB$ và $\triangle IHC$:
\(\widehat{KBH}=\widehat{ICH}\left(\widehat{ABC}=\widehat{ACB}\right)\)
`HB = HC`
\(\widehat{KHB}=\widehat{IHC}\)
$=> \triangle KHB = \triangle IHC (g - c - g)$
`=> BK = CI` `(2` cạnh tương ứng`)`
Ta có:
`AK = AB + BK`
`AI = AC + CI`
Mà `AB = AC; BK = CI`
$=> AK = AI => \triangle AIK$ cân tại A.
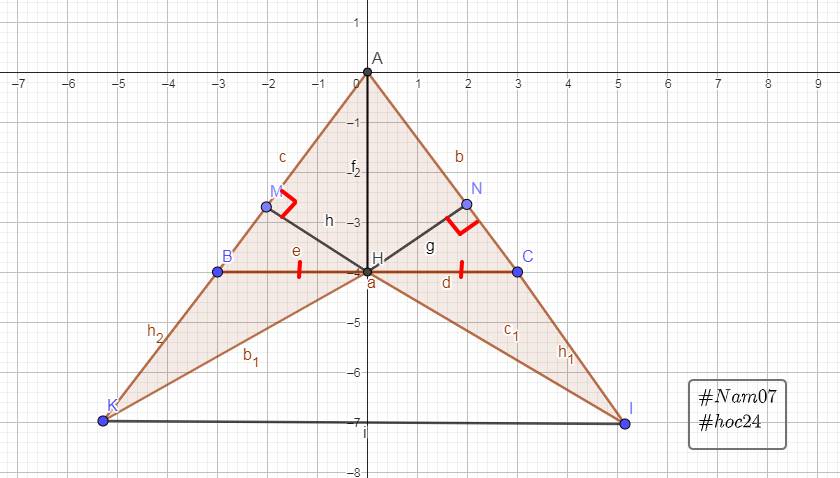

c)Xét \(\Delta\)vuông MHC và \(\Delta\)vuông QHB, ta có:
\(\widehat{MCH}=\widehat{QBH}\)( \(\Delta ABC\)cân tại A)
\(HC=HB\)(chứng minh câu a)
\(\Rightarrow\)\(\Delta\)vuông MHC = \(\Delta\)vuông QHB ( ch-gn)
\(\Rightarrow\widehat{MHC}=\widehat{QHB}\)mà \(\widehat{MHC}=\widehat{BHN}\left(dd\right)\Rightarrow\widehat{QHB}=\widehat{BHN}\)
Gọi K là trung điểm NQ
Xét tam giác KHQ và tam giác KHN, ta có:
HQ=HN( cùng bằng HM)
\(\widehat{QHK}=\widehat{KHN}\)(cmt)
\(HK\): cạnh chung
\(\Rightarrow\)tam giác KHQ = tam giác KHN (c.g.c)
\(\Rightarrow\)\(\widehat{K_1}=\widehat{K_2}=90^o\)và QK = KN \(\Rightarrow HB\)là trung trực của NQ hay là BC là trung trực của NQ.
a) Xét ΔAHM vuông tại M và ΔAHN vuông tại N có
AH chung
\(\widehat{MAH}=\widehat{NAH}\)(AH là tia phân giác của \(\widehat{MAN}\))
Do đó: ΔAHM=ΔAHN(cạnh huyền-góc nhọn)