Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Em tham khảo ở đây:
cho tam giác abc cân tại a nội tiếp đường tròn. d là trung điểm ab e là trọng tâm acd.chứng minh oe vuông góc cd - Hoc24

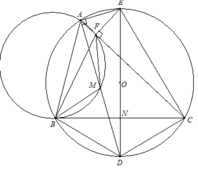
2). Từ AD là phân giác B A C ^ suy ra DB=DC vậy DE vuông góc với BC tại trung điểm N của BC.
Từ 1). Δ B D M ∽ Δ B C F , ta có D M C F = B D B C .
Vậy ta có biến đổi sau D A C F = 2 D M C F = 2 B D B C = C D C N = D E C E (3).
Ta lại có góc nội tiếp A D E ^ = F C E ^ (4).
Từ 3 và 4, suy ra Δ E A D ∽ Δ E F C ⇒ E F C ^ = E A D ^ = 90 ° ⇒ E F ⊥ A C

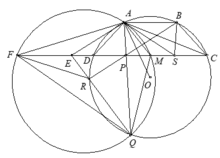
1). Gọi S điểm đối xứng với P qua M.Theo tính chất đối xứng của hình thang cân dễ thấy tứ giác ABSP cũng là hình thang cân.
Ta lại có Q P S ^ = Q A B ^ = Q R B ^ .
Từ đó có E P Q ^ = E R P ^ ⇒ Δ E R P ∽ Δ E P Q (g – g),
nên E Q P ^ = E P R ^ = B P S ^ = A S E ^ , suy ra tứ giác AEQS nội tiếp.
Do đó P A . P Q = P E . P S = P F 2 .2 P M = P F . P M , suy ra tứ giác A M Q F nội tiếp.
Từ đó suy ra đường tròn ngoại tiếp tam giác △ A Q F luôn đi qua M.

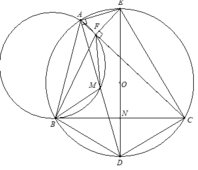
1). Ta có góc nội tiếp bằng nhau B D M ^ = B C F ^ ( 1 ) và B M A ^ = B F A ^ suy ra 180 0 − B M A ^ = 180 0 − B F A ^ hay B M D ^ = B F C ^ (2).
Từ (1) và (2), suy ra Δ B D M ~ Δ B C F (g - g).

A B C A' B' C' I D
\(\overrightarrow{ID}.\overrightarrow{AA'}=\overrightarrow{ID}\left(\overrightarrow{IA'}-\overrightarrow{IA}\right)=\overrightarrow{ID}.\overrightarrow{IA'}-\overrightarrow{ID}.\overrightarrow{IA}=IA'^2-\overrightarrow{ID}.\overrightarrow{IA}\)
\(=IA'^2-\left(\overrightarrow{IC'}+\overrightarrow{C'D}\right)\overrightarrow{IA}=IA'^2-\overrightarrow{IC'}.\overrightarrow{IA'}-\overrightarrow{C'D}.\overrightarrow{IA}=IA'^2-IC'^2-0\) (vì AI vuông góc với C'B')
\(=r^2-r^2=0\) (r là bán kính đường tròn nội tiếp tam giác ABC)
ĐFCM
Cm kiểu vecto ạ
Giải dùm e mai thi rồi ạ