K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên

5 tháng 1 2022
a: Xét tứ giác AHMK có
\(\widehat{AHM}=\widehat{AKM}=\widehat{KAH}=90^0\)
Do đó; AHMK là hình chữ nhật

10 tháng 1 2022
Xét tứ giác AHMK có
\(\widehat{AHM}=\widehat{AKM}=\widehat{KAH}=90^0\)
Do đó: AHMK là hình chữ nhật
mà AM là tia phân giác
nên AHMK là hình vuông

KV
25 tháng 11 2023
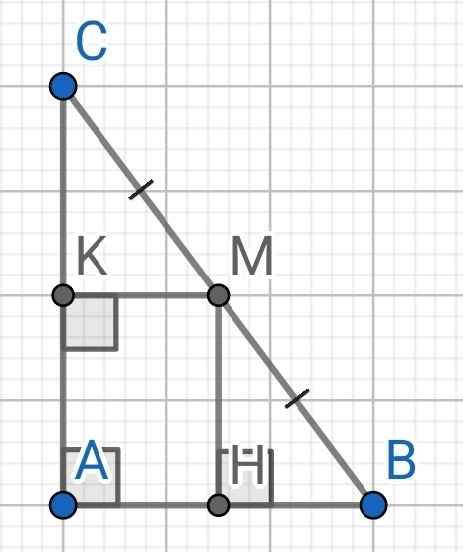 a) Do MH ⊥ AB (gt)
a) Do MH ⊥ AB (gt)
⇒ ∠AHM = 90⁰
Do MK ⊥ AC (gt)
⇒ ∠AKM = 90⁰
Tứ giác AHMK có:
∠AHM = ∠HAK = ∠AKM = 90⁰
⇒ AHMK là hình chữ nhật
b) AB = AC (gt)
⇒ ∆ABC vuông cân tại A
AM là đường trung tuyến
⇒ AM cũng là đường phân giác của ∆BAC
⇒ AM là đường phân giác của ∠HAK
Ta có:
AHMK là hình chữ nhật (cmt)
AM là đường phân giác của ∠HAK (cmt)
⇒ AHMK là hình vuông