Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Xét ΔAMB và ΔAMC co
AM chung
MB=MC
AB=AC
=>ΔAMB=ΔAMC
=>góc MAB=góc MAC
Xét ΔAEM vuông tại E và ΔAFM vuông tại F có
AM chung
góc EAM=góc FAM
=>ΔAEM=ΔAFM
=>AE=AF và ME=MF
b: Xét ΔABC có AE/AB=AF/AC
nên EF//BC

a: Xét ΔAMB và ΔAMC co
AM chung
MB=MC
AB=AC
=>ΔAMB=ΔAMC
=>góc MAB=góc MAC
Xét ΔAEM vuông tại E và ΔAFM vuông tại F có
AM chung
góc EAM=góc FAM
=>ΔAEM=ΔAFM
=>AE=AF và ME=MF
b: Xét ΔABC có AE/AB=AF/AC
nên EF//BC
c: IN//EM
=>NI/ME=BN/BM
=>NI/MF=BN/CM
=>NI/BN=MF/CM
FM//NK
=>MF/NK=CM/CN
=>MF/CM=NK/CN
=>NK/CN=NI/BN=(NI+NK)/BC ko đổi

a: Xét ΔAMB và ΔAMC co
AM chung
MB=MC
AB=AC
=>ΔAMB=ΔAMC
=>góc MAB=góc MAC
Xét ΔAEM vuông tại E và ΔAFM vuông tại F có
AM chung
góc EAM=góc FAM
=>ΔAEM=ΔAFM
=>AE=AF và ME=MF
b: Xét ΔABC có AE/AB=AF/AC
nên EF//BC
c: IN//EM
=>NI/ME=BN/BM
=>NI/MF=BN/CM
=>NI/BN=MF/CM
FM//NK
=>MF/NK=CM/CN
=>MF/CM=NK/CN
=>NK/CN=NI/BN=(NI+NK)/BC ko đổi

a: Xét ΔAMB và ΔAMC co
AM chung
MB=MC
AB=AC
=>ΔAMB=ΔAMC
=>góc MAB=góc MAC
Xét ΔAEM vuông tại E và ΔAFM vuông tại F có
AM chung
góc EAM=góc FAM
=>ΔAEM=ΔAFM
=>AE=AF và ME=MF
b: Xét ΔABC có AE/AB=AF/AC
nên EF//BC
c: IN//EM
=>NI/ME=BN/BM
=>NI/MF=BN/CM
=>NI/BN=MF/CM
FM//NK
=>MF/NK=CM/CN
=>MF/CM=NK/CN
=>NK/CN=NI/BN=(NI+NK)/BC ko đổi

a: Xét ΔAMB và ΔAMC có
AM chung
MB=MC
AB=AC
Do đó: ΔAMB=ΔAMC
b:Sửa đề: Chứng minh AE=AF
Ta có: ΔAMB=ΔAMC
=>\(\widehat{AMB}=\widehat{AMC}\)
mà \(\widehat{AMB}+\widehat{AMC}=180^0\)(hai góc kề bù)
nên \(\widehat{AMB}=\widehat{AMC}=\dfrac{180^0}{2}=90^0\)
=>AM\(\perp\)BC
Ta có: ΔABM=ΔACM
=>\(\widehat{BAM}=\widehat{CAM}\)
Xét ΔAEM vuông tại E và ΔAFM vuông tại F có
AM chung
\(\widehat{EAM}=\widehat{FAM}\)
Do đó: ΔAEM=ΔAFM
=>AE=AF
c: Xét ΔABC có \(\dfrac{AE}{AB}=\dfrac{AF}{AC}\)
nên EF//BC
d: Xét ΔABN vuông tại B và ΔACN vuông tại C có
AN chung
AB=AC
Do đó: ΔABN=ΔACN
=>BN=CN
=>N nằm trên đường trung trực của BC(1)
Ta có; ΔABC cân tại A
mà AM là đường trung tuyến
nên AM là đường trung trực của BC(2)
Từ (1) và (2) suy ra A,M,N thẳng hàng

a, Vì Tam giác `ABC` cân tại A `=> AB = AC ;`\(\widehat{B}=\widehat{C}\)
Xét Tam giác `AMB` và Tam giác `AMC` có:
`AM chung`
\(\widehat{B}=\widehat{C}\) `(CMT)`
`MB = MC (g``t)`
`=>` Tam giác `AMB =` Tam giác `AMC (c-g-c)`
b, Vì Tam giác `AMB =` Tam giác `AMC (a)`
`=>` \(\widehat{EAM}=\widehat{FAM}\) (2 góc tương ứng).
Xét Tam giác `EAM` và Tam giác `FAM` có:
AM chung
\(\widehat{EAM}=\widehat{FAM}\) `(CMT)`
\(\widehat{AEM}=\widehat{AFM}=90^0\)
`=>` Tam giác `EAM =` Tam giác `FAM (ch-gn)`
`=> EA = FA` (2 cạnh tương ứng).
c, *câu này mình hơi bí bn ạ:')
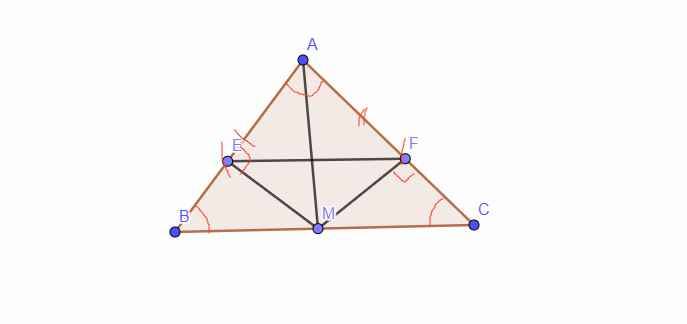
a: Xét ΔAMB và ΔAMC có
AM chung
MB=MC
AB=AC
Do đó: ΔAMB=ΔAMC
b: Xét ΔAEM vuông tại E và ΔAFM vuông tại F có
AM chung
góc EAM=góc FAM
Do đó: ΔAEM=ΔAFM
=>AE=AF
c: Xét ΔABC có AE/AB=AF/AC
nên EF//BC

a: Xét ΔEBM vuông tại E và ΔFCM vuông tại F có
MB=MC
góc B=góc C
=>ΔEBM=ΔFCM
b: Xet ΔAEM vuông tại E và ΔAFM vuông tại F có
AM chung
ME=MF
=>ΔAEM=ΔAFM
=>AE=AF
mà ME=MF
nên AM là trung trực của EF
c: Xét ΔABC có AE/AB=AF/AC
nên EF//BC
d: Xet ΔABD vuông tại B và ΔACD vuông tại C có
AD chung
AB=AC
=>ΔABD=ΔACD
=>BD=CD
=>D nằm trên trung trực của BC
=>A,M,D thẳng hàng

A B C M I E F
a) _ Xét tam giác AME và tam giác AMF có :
E = F ( = 90 độ)
AM là cạnh huyền chung
A1=A2 ( AM là tia phân giác của BAC)
suy ra : tam giác AME = tam giác AMF ( CH-GN)
suy ra AE = AF ( 2 cạnh tương ứng)
suy ra tam giác AEF cân tại A
vẽ hình tạm nha
~ chúc bn học tốt~
a: Xét ΔAMB và ΔAMC co
AM chung
MB=MC
AB=AC
=>ΔAMB=ΔAMC
=>góc MAB=góc MAC
Xét ΔAEM vuông tại E và ΔAFM vuông tại F có
AM chung
góc EAM=góc FAM
=>ΔAEM=ΔAFM
=>AE=AF và ME=MF
b: Xét ΔABC có AE/AB=AF/AC
nên EF//BC
c: IN//EM
=>NI/ME=BN/BM
=>NI/MF=BN/CM
=>NI/BN=MF/CM
FM//NK
=>MF/NK=CM/CN
=>MF/CM=NK/CN
=>NK/CN=NI/BN=(NI+NK)/BC ko đổi