

Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



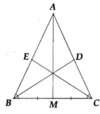
a) Chứng minh được ∆ A M B = ∆ A M C (c.c.c).
Từ đó suy ra AM là tia phân giác của góc BAC.
b) Xét tam giác ABC có AM, BD,CE là các tia phân giác. Từ tính chất ba đường phân giác trong tam giác, suy ra ba đường thẳng AM,BD,CE đồng quy.

tự vẽ hình nha
a, Xét tg ABD và tg ACE có:
AB=AC (gt)
góc A chung
góc ADB = góc AEC (=90)
=>tg ABD = tg ACE (ch-gn)
=>BD=CE (1)
b, Xét tg OAD và tg OAE có;
AD=AE (tg ABD = tg ACE)
OA chung
góc ODA = góc OED (=90)
=>tg OAD = tg OAE (ch-cgv)
=>OD=OE (2)
Từ (1),(2) => BD - OD = CE - OE hay OB = OC
c, từ tg OAD = tg OAE (câu b) => góc OAD = góc OAE
Mà tia OA nằm giữa 2 góc này
=> OA là tia pg của góc BAC
d, Xét tg ABC cân tại A có: \(\widehat{B}=\widehat{C}=\frac{180^o-\widehat{A}}{2}\) (3)
Lại có AD=AE (tg ABD = tg ACE) => tg ADE cân tại A => \(\widehat{ADE}=\widehat{AED}=\frac{180-\widehat{A}}{2}\) (4)
Từ (3),(4) => \(\widehat{B}=\widehat{C}=\widehat{ADE}=\widehat{AED}\) hay góc B = góc AED
mà 2 góc này ở vị trí đồng vị
=>DE//BC

Sửa đề: M là trung điểm của BC
a: ΔABC cân tại A có AM là trung tuyến
nên AM là phân giác của góc BAC
b: Xét ΔABC có
AM,BD,CE là các đường phân giác
=>AM,BD,CE đồng quy tại H

https://h.vn/hoi-dap/question/168197.html
tham khảo nhé bạn