Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

tu ve hinh :
a; b, xet tamgiac AMF va tamgiac AME co : AM chung
goc AFM = goc AEM = 90 do MF | AC va ME | AB (gt)
goc FAM = goc EAM do AM la phan giac cua goc BAC (gt)
=> tamgiac AMF = tamgiac AME (ch - gn)
=> AE = AF (dn) (1)
AB = AC do tamgiac ABC can tai A (gt)
AE + EB = AB
AF + FC = AC
=> EB = FC
xet tamgiac BEM va tamgiac CFM co : goc B = goc C do tamgiac ABC can tai A (gt)
goc MEB = goc MFC do ...
=> tamgiac BEM = tamgiac CFM (cgv - gnk)
=> MB = MC
c, (1) => tamgiac AEF can tai E (dn)
=> goc AEF = (180 - goc BAC) : 2
tamgiac ABC can tai A (gt) => goc B = (180 - goc BAC) : 2
=> goc AEF = goc B ma 2 goc nay dong vi
=> EF // BC (dh)
Giải
Bạn tự vẽ hình
a; b, Xét \(\Delta AMF\) va \(\Delta AME\) có : AM chung
\(\widehat{AFM}=\widehat{AEM}=90^0\) do MF\(\perp\)AC va ME\(\perp\)AB
\(\widehat{FAM}=\widehat{EAM}\)do AM la phân giác của \(\widehat{BAC}\)
\(\Rightarrow\Delta AFM=\Delta AME\)
\(\Rightarrow AE=AF\) (1)
AB = AC do \(\Delta ABC\) cân tại A
AE + EB = AB
AF + FC = AC
\(\Rightarrow\) EB = FC
Xét \(\Delta BEM\) và \(\Delta CFM\) có : \(\widehat{B}\) = \(\widehat{C}\) do \(\Delta ABC\) cân tại A
\(\Rightarrow\widehat{MEB}=\widehat{MFC}\)
\(\Rightarrow\Delta BEM=\Delta CFM\)
\(\Rightarrow\) MB = MC
c, Từ (1) suy ra \(\Delta AEF\)cân tại E
\(\Rightarrow\widehat{AEF}=\left(180-\widehat{BAC}\right)\div2\)
\(\Delta ABC\) cân tại A \(\Rightarrow\)\(\widehat{B}\)= (180 - \(\widehat{BAC}\)) : 2
\(\Rightarrow\widehat{AEF}=\widehat{B}\) mà hai góc này đồng vị
\(\Rightarrow EF//BC\)

A B C M N 1 2 2 1 E F 1 1 2 2 O
CM : a) Ta có: t/giác ABC cân tại A
=> góc B2 = góc C2
Mà góc B1 + góc B2 = 1800
góc C1 + góc C2 = 1800
=> góc B1 = góc C1
Xét t/giác AMB và t/giác ANC
có AB = AC (gt)
góc B1 = góc C1 (cmt)
MB = NC (gt)
=> t/giác AMB = t/giác ANC (c.g.c)
=> AM = AN (hai cạnh tương ứng)
=> t/giác AMN là t/giác cân tại A
b) Ta có: t/giác AMN cân tại A
=> góc M = góc N
Xét t/giác BME và t/giác CNF
có góc E1 = góc F1 = 900 (gt)
BM = CN (gt)
góc M = góc N (cmt)
=> t/giác BME = t/giác CNF (cạnh huyền - góc nhọn)
c,d) tự làm

Hình tự kẻ nha
a)Xét 2 tam giác vuông ABH và ACH có
Góc AHB = góc AHC (=90°)
AB= AC ( tam giác ABC cân tại A)
Góc ABC = góc ACB (tam giác ABC cân tại A)
=>2 tam giác vuông ABH=ACH (cạnh huyền -góc nhọn)
b)Tam giác ABC cân =>góc ABC=gócACB
=>gócABM=gócACN
Xét 2 tam giác ABM và ACN
AB=AC ( tam giác ABC cân tại A)
Góc ABM=góc ACN (cmt)
BM=CN(gt)
=> tam giác ABM=tam giác ACN
=>AM=AN
Do đó tam giác AMN cân tại A
c) Phần này hình như sai đề
A B C M N H E F K 1 2 1 1 2 3 3 2
a) Xét t/giác ABH và t/giác ACH
có: AB = AC (gt)
\(\widehat{H_1}=\widehat{H_2}=90^0\)(gt)
\(\widehat{B_1}=\widehat{C_1}\) (gt)
=> t/giác ABH = t/giác ACH (ch - gn)
b) Ta có: \(\widehat{B_1}+\widehat{ABM}=180^0\)(kề bù)
\(\widehat{C_1}+\widehat{ACN}=180^0\) (kề bù)
Mà \(\widehat{B_1}=\widehat{C_1}\) (gt) => \(\widehat{ABM}=\widehat{ACN}\)
Xét t/giác ABM và t/giác ACN
có AB = AC (gt)
\(\widehat{ABM}=\widehat{ACN}\) (cmt)
BM = CN (gt)
=> t/giác ABM = t/giác ACN (c.g.c)
=> AM = AN (2 cạnh t/ứng)
=> t/giác AMN cân
c) Ta có: t/giác MEB vuông tại A => \(\widehat{M}+\widehat{B_2}=90^0\)
t/giác FCN vuông tại F => \(\widehat{C_2}+\widehat{N}=90^0\)
Mà \(\widehat{M}=\widehat{N}\)(Vì t/giác AMN cân tại A) => \(\widehat{B_2}=\widehat{C_2}\) (1)
Ta lại có: \(\widehat{B_2}=\widehat{B_3}\) (Đối đỉnh); \(\widehat{C_2}=\widehat{C_3}\)(đối đỉnh) (2)
Từ (1) và (2) => \(\widehat{B_3}=\widehat{C_3}\) => t/giác BKC cân tại K
có KH là đường cao
=> KH cũng là đường trung trực của cạnh BC (t/c của t/giác cân) (3)
(đoạn này chưa học có thể xét t/giác KBH và t/giác KCH => BH = CH => KH là đường trung trực)
t/giác ABH = t/giác ACH (cm câu a) => BH = CH
=> AH là đường trung tuyến
mà AH cũng là đường cao
=> AH là đường trung trực của cạnh BC (4)
Do A \(\ne\)K (5)
Từ (3); (4); (5) => A, H, K thẳng hàng

a: Xét tứ giác AQHP có
AQ//HP
AP//HQ
=>AQHP là hình bình hành
Xet ΔAHQ và ΔHAP có
HA chung
HQ=AP
AQ=HP
=>ΔAHQ=ΔHAP
b: ΔFBC vuông tại F
mà FM là trung tuyến
nên FM=BC/2
ΔECB vuông tại E
mà EM là trung tuyến
nên EM=BC/2=FM
=>ΔMEF cân tại M
góc BFC=góc BEC=90 độ
=>BFEC nội tiếp
=>góc AEF=góc ABC
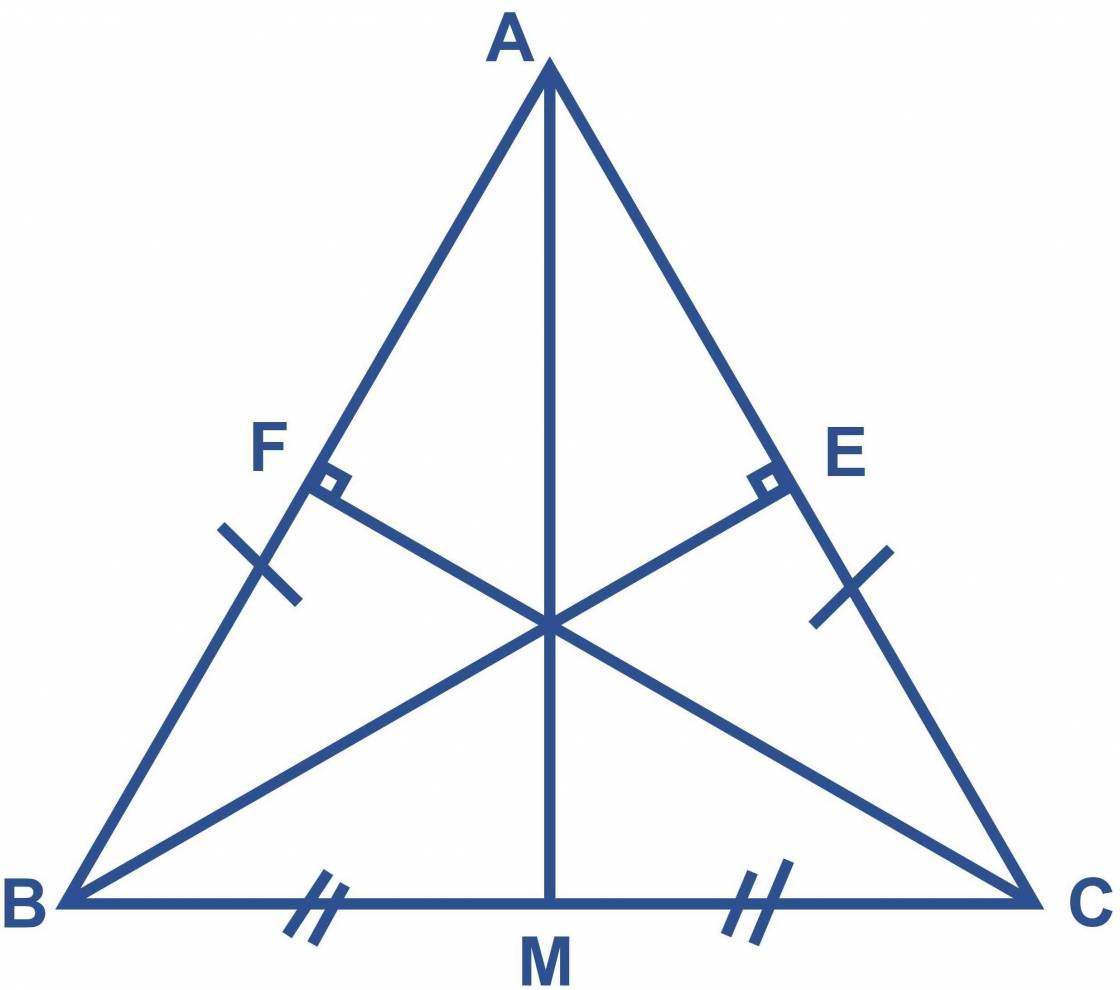
A B C E F M D N
a) Vì \(\Delta ABC\) cân tại A nên AB = AC và Góc B = Góc C. Vì \(BE\perp AC;CF\perp AB\left(gt\right)\)
Nên ^AFC = ^BFC = ^AEB = ^CEB = 900. Xét \(\Delta AFC\) và \(\Delta AEB\) có :
^AFC = ^AEB = 900; \(AC=AB\left(cmt\right)\); Góc O chung. \(\Rightarrow\Delta AFC=\Delta AEB\left(ch.gn\right)\)
b) \(\Rightarrow AF=AE\) ( 2 cạnh tương ứng ). Có ^AFC = ^AEB hay ^AFD = ^AED = 900
Xét \(\Delta AED\) và \(\Delta AFD\) có : ^AFD = ^AED = 900 ( cmt ) ; \(AF=AE\left(cmt\right);AD\) chung
\(\Rightarrow\Delta AED=\Delta AFD\left(ch.cgv\right)\Rightarrow\) ^EAD = ^FAD ( tương ứng ) nên AD là phân giác ^FAE ( đpcm )
c) Gọi giao điểm của AM và DE tại N. Xét \(\Delta AEN\) và \(\Delta AFN\) có :
\(AE=AF\left(cmt\right)\); ^EAN = ^FAN ( ^EAD = ^FAD ); \(AN\) chung.
\(\Rightarrow\Delta AEN=\Delta AFN\left(c.g.c\right)\Leftrightarrow\) ^ANE = ^ANF ( tương ứng ). Mà ^ANE + ^ANF = 1800 ( kề bù )
=> ^ANE = ^ANF = 1800 : 2 = 900 \(\Leftrightarrow AN\perp FE\). Mà N là giao điểm của AM và FE
Nên N thuộc AM \(\Rightarrow AN\perp FE\Leftrightarrow AM\perp FE\left(đpcm\right)\)
Ờ ! viết bằng nhau ''='' thật đấy, nhưng trên hình kí hiệu j đâu mà viết nó ''='' nhau
LOGIC ?
Cái deck j vại, bn nhìn thấy ^O ở đâu thế bn Minh !
Ý thức ko mua đc ''='' tiền.