Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ta có hình vẽ:
A B C N M
Theo bài ra ta có:
Tam giác ABC cân tại A
=> AB=AC ( hai cạnh bên của tam giác cân )
Ta lại có:
M là trung điểm của AC;N là trung điểm của AB
=> AN=BN=CM=AM
Ta có: \(\Delta ABM=\Delta ACN\) (c.g.c)
=> BM=CN ( hai cạnh tuơng ứng )
(đ.p.c.m)

\(\hept{\begin{cases}AB=AC\\AM=\frac{1}{2}AC\\AN=\frac{1}{2}AB\end{cases}}\)
Từ đó suy ra AM=AN
=>BM=CN
ta có tam giác ABC cân tại A => AB=AC ( hai cạnh bên)
mà ta có AM =MC (vì m là trung điểm) => mc=\(\frac{1}{2}ac\)
ta lại có an =nb (vì n là trung điểm ab)=> nb=\(\frac{1}{2}ab\) mà ab=ac=> 1/2 ab=1/2ac hay mc=bn
xét tam giác bnc và tam giác cmb có:
bn=mc(cmt)
góc nbc=góc mcb
bc chung
do đó tam giác bnc = tam giác cmb (c.g.c)
=>nc=bm (hai cạnh tương ứng)
thông cảm hình vẽ quá xấu mình chắc chắn đúng đó

Xét ΔAMB và ΔAMC có
AM chung
MB=MC
AB=AC
Do đó; ΔAMB=ΔAMC
=>\(\hat{MAB}=\hat{MAC}\)
Xét ΔADM vuông tại D và ΔAEM vuông tại E có
AM chung
\(\hat{DAM}=\hat{EAM}\)
Do đó: ΔADM=ΔAEM
=>AD=AE
=>ΔADE cân tại A
ΔADE cân tại A
=>\(\hat{ADE}=\frac{180^0-\hat{DAE}}{2}=\frac{180^0-\hat{BAC}}{2}\left(1\right)\)
ΔABC cân tại A
=>\(\hat{ABC}=\frac{180^0-2\cdot\hat{BAC}}{2}\left(2\right)\)
Từ (1),(2) suy ra \(\hat{ADE}=\hat{ABC}\)
mà hai góc này là hai góc ở vị trí đồng vị
nên DE//BC

Xét tam giác ABM và ACN
A la goc chung
AB=AC
AN=AM( deu la trung diem cua 2 canh bang nhau
=>Tam giac ABM=ACN=> BM=CN(dpcm)
+) Do M là trung điểm của AC nên: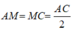 (1)
(1)
+) Do N là trung điểm của AB nên: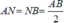 (2)
(2)
Lại có: AB = AC ( vì tam giác ABC cân tại A). (3)
Từ (1); (2); (3) suy ra: AN = NB = AM = MC.
+) Xét ∆ AMB và ∆ANC có:
Góc A chung
AM = AN ( chứng minh trên)
AB = AC ( vì tam giác ABC cân tại A)
Suy ra: ∆ AMB = ∆ANC ( c.g.c)
Do đó: BM = CN ( hai cạnh tương ứng).