Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
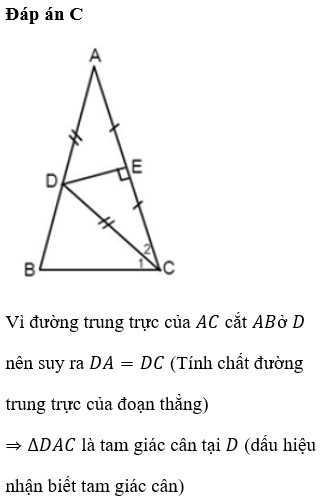
Bài làm
a) Xét ∆ABC vuông tại B có:
^BAC + ^C = 90°
Hay ^BAC + 30° = 90°
=> ^BAC = 60°
Vì AD là phân giác của góc BAC.
=> ^DAC = 60°/2 = 30°
Xét tam giác ADC có:
^DAC + ^ACD + ^ADC = 180°
Hay 30° + 30° + ^ADC = 180°
=> ^ADC = 180° - 30° - 30°
=> ^ADC = 120°
b) Xét tam giác ABD và tam giác AED có:
AB = AE ( gt )
^BAD = ^EAD ( Do AD phân giác )
Cạnh AD chung.
=> ∆ABD = ∆AED ( c.g.c )
c) Vì ∆ABD = ∆AED ( cmt )
=> ^ABD = ^AED = 90°
=> DE vuông góc với AC tại E (1)
Ta có: ^DAC = ^DCA = 30°
=> ∆DAC cân tại D.
=> AD = DC
Xét tam giác DEA và tam giác DEC có:
Góc vuông: ^DEA = ^DEC ( = 90° )
Cạnh huyền AD = DC ( cmt )
Góc nhọn: ^DAC = ^DCA ( cmt )
=> ∆DEA = ∆DEC ( g.c.g )
=> AE = EC
=> E là trung điểm của AC. (2)
Từ (1) và (2) => DE là trung trực của AC ( đpcm )
Đã vẽ hình và tính giúp bạn. Kết quả bằng cả suy luận và kiểm tra số học:
\(\angle A M C = 180^{\circ} - 50^{\circ} - 30^{\circ} = 100^{\circ} .\)
\(\angle B M C = 180^{\circ} - 70^{\circ} - 30^{\circ} = 80^{\circ} .\)
(Thỏa mãn \(\angle A M C + \angle B M C = 180^{\circ}\) vì \(A , M , B\) thẳng hàng.)
Mình cũng đã vẽ hình minh họa (tam giác ABC và tia phân giác \(C M\) cắt \(A B\) tại \(M\)) — xem ảnh kèm. Bạn cần mình ghi lời giải hoàn chỉnh theo dạng nộp bài (có LaTeX, lời văn) không?
Bài 2:
\(\widehat{ADB}=180^0-80^0=100^0\)
Ta có: \(\widehat{ADB}+\widehat{BAD}+\widehat{B}=\widehat{ADC}+\widehat{CAD}+\widehat{C}\)
\(\Leftrightarrow\widehat{B}+100^0=\widehat{C}+80^0\)
\(\Leftrightarrow1.5\widehat{C}-\widehat{C}=-20^0\)
\(\Leftrightarrow\widehat{C}=40^0\)
hay \(\widehat{B}=60^0\)
=>\(\widehat{BAC}=80^0\)
Vì CD và CE là hai tia phân giác của hai góc kề bù
nên CD⊥CE
=>ΔDCE vuông tại C
Xét ΔADC có \(\hat{BDC}\) là góc ngoài tại đỉnh D
nên \(\hat{BDC}=\hat{DAC}+\hat{DCA}=\hat{BAC}+\frac12\cdot\hat{ACB}\)
\(=\hat{BAC}+\frac12\left(180^0-\hat{BAC}-\hat{ABC}\right)=90^0+\frac12\cdot\hat{BAC}-\frac12\cdot\hat{ABC}\)
Xét ΔDCE vuông tại C có \(\hat{CDE}+\hat{CED}=90^0\)
=>\(\hat{CED}=90^0-\left(90^0+\frac12\cdot\hat{BAC}-\frac12\cdot\hat{ABC}\right)=-\frac12\cdot\hat{BAC}+\frac12\cdot\hat{ABC}\)
Kết quả:
\(\angle C E D = \frac{\mid A - B \mid}{2} .\)Giải nhanh: Gọi \(C = 180^{\circ} - A - B\). Vì \(C E\) là tia phân giác góc ngoài tại \(C\), nên nó tạo với \(C A\) một góc
\(\hat{\left(\right. C E , C A \left.\right)} = 90^{\circ} - \frac{C}{2} .\)Qua \(E\) kẻ đường thẳng song song với \(C A\); đường này tạo với \(A B\) một góc bằng \(A\). Do đó góc giữa \(C E\) và \(A B\) (chính là \(\angle C E D\)) bằng
\(\mid \textrm{ } A - \left(\right. 90^{\circ} - \frac{C}{2} \left.\right) \mid .\)Thay \(C = 180^{\circ} - A - B\) vào, ta có \(90^{\circ} - \frac{C}{2} = \frac{A + B}{2}\). Suy ra
\(\angle C E D = \mid A - \frac{A + B}{2} \mid = \frac{\mid A - B \mid}{2} .\)(Với quy ước lấy góc nhọn tại \(E\); nếu \(A \geq B\) thì \(\angle C E D = \frac{A - B}{2}\), còn nếu \(A < B\) thì \(\angle C E D = \frac{B - A}{2}\).)
a/
Do \(\Delta ABC\) cân\(\widehat{ABC}=\widehat{ACB}\)
\(\widehat{DBC}+\widehat{ABC}=\widehat{DCB}+\widehat{ACB}=90^o\Rightarrow\widehat{DBC}=\widehat{DCB}\Rightarrow\Delta BDC\) cân tại D
b/
Ta có \(\Delta BDC\) cân nên\(BD=CD\)
\(\Delta ABC\) cân nên \(AB=AC\)
\(\Rightarrow\Delta ABD=\Delta ACD\) (Hai tg vuông có các cạnh góc vuông tương ứng bằng nhau)
\(\Rightarrow\widehat{BAD}=\widehat{CAD};\widehat{BDA}=\widehat{CDA}\) => AD là phân giác của \(\widehat{A}\) và \(\widehat{D}\)
c/
Do tg ABC cân tại A và AD là phân giác \(\widehat{A}\) nên AD là đường cao đồng thời là đường trung tuyến thuộc cạnh BC của tg ABC (Trong tg cân đường phân giác đồng thời là đường cao, đường trung tuyến và đường trung trực)
\(\Rightarrow AD\perp BC\) và đi qua trung điểm của BC
