K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên

CM
22 tháng 11 2017
Chứng minh được ADME là hình bình hành Þ I là trung điểm của AM. Tương tự 2A. I thuộc đường trung bình của D ABC (đường thẳng đi qua trung điểm của AB và AC)
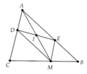

20 tháng 3 2018
Do DE // BC
\(\Rightarrow\)\(\frac{DE}{BC}\)=\(\frac{AD}{AB}\)(Hệ quả Ta lét)
Mà AD=BM (gt)
Suy ra : \(\frac{AD}{AB}\)=\(\frac{BM}{AB}\)
\(\Rightarrow\)\(\frac{DE}{BC}\)=\(\frac{BM}{AB}\)
\(\Rightarrow\)DE=\(\frac{BC.BM}{AB}\)
Xét \(\Delta ABC\)có MN//BC
\(\frac{MN}{BC}\)=\(\frac{AM}{AB}\)(Hệ quả Talét)
\(\Rightarrow\)MN=\(\frac{BC.AM}{AB}\)
Suy ra DE+MN=\(\frac{BC.BM}{AB}\)+ \(\frac{BC.AM}{AB}\)
\(\Rightarrow\)DE+MN=\(\frac{BC.AB}{AB}\)= BC
Mà BC là đường cố định không đổi
\(\Rightarrow\)DE+MN không đổi