Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Xét ΔAEF và ΔDFE có
góc AEF=góc DFE
EF chung
góc AFE=góc DEF
Do đó: ΔAEF=ΔDFE
Xét ΔEDC có góc EDC=góc ECD
nên ΔEDC cân tại E
=>ED=CE=3-AE
Xét ΔFBD có góc FDB=góc FBD
nên ΔFBD cân tại F
=>FD=FB=3-AF=3-DE=3-EC
ED+FD=3-AE+3-DE=3-AE+3-EC=6-3=3cm

Xét ΔAEF và ΔDFE có
góc AEF=góc DFE
EF chung
góc AFE=góc DEF
Do đó: ΔAEF=ΔDFE
Xét ΔEDC có góc EDC=góc ECD
nên ΔEDC cân tại E
=>ED=CE=3-AE
Xét ΔFBD có góc FDB=góc FBD
nên ΔFBD cân tại F
=>FD=FB=3-AF=3-DE=3-EC
ED+FD=3-AE+3-DE=3-AE+3-EC=6-3=3cm

Xét ΔAEF và ΔDFE có
góc AEF=góc DFE
EF chung
góc AFE=góc DEF
Do đó: ΔAEF=ΔDFE
Xét ΔEDC có góc EDC=góc ECD
nên ΔEDC cân tại E
=>ED=CE=3-AE
Xét ΔFBD có góc FDB=góc FBD
nên ΔFBD cân tại F
=>FD=FB=3-AF=3-DE=3-EC
ED+FD=3-AE+3-DE=3-AE+3-EC=6-3=3cm

 (hình 138).DE//AF, DF//AE nên DE=AF (1) (giải thích như bài 52)
(hình 138).DE//AF, DF//AE nên DE=AF (1) (giải thích như bài 52)
DF//AC\(\Rightarrow\) \(\widehat{D1}=\widehat{C}\) (đồng vị)
\(\Delta ABC\) cân tại A\(\Rightarrow\)\(\widehat{B}=\widehat{C}\)
Suy ra :\(\widehat{D1}=\widehat{B}\)
\(\Delta FBD\) có \(\widehat{D1}=\widehat{B}\) suy ra \(\Delta FBD\) cân tại F \(\Rightarrow\)FB=FD (2)
Từ (1) và (2)\(\Rightarrow\)DE+DF=AF+FB=AB=3cm

Ta có hình vẽ

Ta có:
FD//EC và BF//ED
=> +) \(\widehat{FDB}=\widehat{ECD}\) (hai góc đồng vị ) (1)
+) \(\widehat{FBD}=\widehat{EDC}\) (hai góc đồng vị ) (2)
+)\(\widehat{DFB}=\widehat{FDE}\) (hai góc đồng vị )
+)\(\widehat{FDE}=\widehat{DFE}\) (hai góc đồng vị )
+)\(\widehat{EBF}=\widehat{DEC}\) (hai góc đồng vị )
+)\(\widehat{EDC}=\widehat{DEF}\) (hai góc đồng vị )
Ta lại có :
\(\Delta ABC\) cân tại A => \(\widehat{B}=\widehat{C}\) ( hai góc ở đáy của tam giác cân ) (3)
Từ (1);(2) và (3) ta suy ra:
+)\(\Delta FBD\) là tam giác cân tại F ( vì tam giác có 2 góc bằng nhau )
+)\(\Delta EDC\) là tam giác cân tại E ( vì tam giác có 2 góc bằng nhau )
=> +) FB=FD (4)
+) ED=EC (5)
Ta lại có:
*)\(\Delta FBD=\Delta DEF\) (g.c.g)
=> +) FB=ED ( hai cạnh tuơng ứng ) (6)
+) BD=FE ( hai cạnh tuơng ứng ) (7)
*)\(\Delta DFE=\Delta ECD\) (g.c.g)
=> +) FD=EC ( hai cạnh tuơng ứng ) (8)
+) FE=DC ( hai cạnh tuơng ứng ) (9)
Từ(4);(5);(6) và (8) suy ra:
FB=FD=DE=EC (10)
Ta lại có:
\(\Delta FBD=\Delta AFE\) (g.c.g)
=> AF=BF ( hai cạnh tương ứng ) (11)
=> \(AF=\dfrac{1}{2}AB=\dfrac{1}{2}.3=\dfrac{3}{2}=1,5\) (12)
Từ (10) và (11) suy ra:
AF=FD=ED (13)
Từ (12) và (13) suy ra:
FD=ED=1,5 (cm)
=> FD+ED=3 (cm)
Vậy DE+DF=3 (cm)

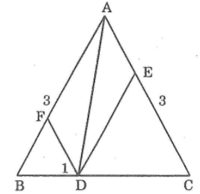
Ta có: DF // AC(gt)
=> ∠D1 = ∠C (hai góc đồng vị) (1)
Lại có: ΔABC cân tại A
=> ∠B = ∠C (tính chất tam giác cân) (2)
Từ (1) và (2) suy ra: ∠B = ∠D1
Hay ΔBFD cân tại F =>BF = DF (3)
Nối AD. Xét ΔAFD và ΔDEA có:
∠ADF =∠EAD(so le trong vì DF // AC)
AD cạnh chung
∠DAF =∠ADE (so le trong vì DE // AB)
Suy ra: ΔAFD= ΔDEA(g.c.g)
Nên AF = DE (hai cạnh tương ứng) (4)
Từ(3) và (4) suy ra: DE + DF = AF + BF = AB = 3cm

Xét ΔAEF và ΔDFE có
góc AEF=góc DFE
EF chung
góc AFE=góc DEF
Do đó: ΔAEF=ΔDFE
Xét ΔEDC có góc EDC=góc ECD
nên ΔEDC cân tại E
=>ED=CE=3-AE
Xét ΔFBD có góc FDB=góc FBD
nên ΔFBD cân tại F
=>FD=FB=3-AF=3-DE=3-EC
ED+FD=3-AE+3-DE=3-AE+3-EC=6-3=3cm


