Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

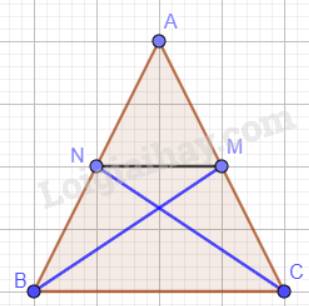
Tam giác ABC cân tại A nên AB = AC.
M và N lần lượt là trung điểm của AC và AB nên:
\(\begin{array}{l}AN = BN = \dfrac{1}{2}AB\\AM = CM = \dfrac{1}{2}AC\end{array}\)
Mà AB = AC nên AN = BN = AM = CM.
Xét tam giác AMB và tam giác ANC có:
\(\widehat A\)chung;
AB = AC (cmt);
AM = AN (cmt).
Vậy \(\Delta AMB = \Delta ANC\)(c.g.c) nên BM = CN ( 2 cạnh tương ứng).

a)
ta có: AB=AC suy ra 1/2 AB=1/2AC suy ra AN=NB=AM=MC
xét tam giác ABM và tam giác ACN có:
AB=AC
AM=AN(cmt)
A(chung)
suy ra tam giác ABM=ACN(c.g.c)
suy ra BM=CN
b)
ta có: I là trọng tâm cua tam giác ABC
ta có: MB=NC(theo câu a) suy ra 2/3MB=2/3NC suy ra IB=IC suy ra tam giac IBC cân tại I
c)
xét tam giác AIB và tam giác AIC có:
AB=AC
AI(chung)
IB=IC
suy ra tam giác AIB=AIC(c.c.c)
suy ra BAI=CAI
suy ra AI là phân giác của góc A

a) tam giác ABC vuông tại A
=> AB2 + AC2 = BC2 (định lý py-ta-go)
=> 92 + AC2 = 152
=> AC2 = 225 - 81
=> AC2 = 144 => AC = \(\sqrt{144}=12cm\)
t i c k đúng nhé
a) trong tam giác ABC có: AB < AC < BC ( 9 < 12 < 15)
=> góc C < góc B < góc A (định lý)

Câu 1:
Xét tam giác AMB và tam giác AMC ta có:
AB = AC (tam giác ABC cân tại A)
ABM = ACM (tam giác ABC cân tại A)
=> Tam giác AMB = tam giác AMC (ch-gn) (dpcm)
Câu 2:
a) Ta có: +) AK+KB = AB => KB = AB-AK
+) AH+HC = AC => HC = AC-AH
Mà AB=AC(tam giác ABC cân tại A) ; AK=AH (gt)
=>KB=HC
Xét tam giác BHC và tam giác CKB ta có:
HC=KB (cmt)
HCB=KBC (tam giác ABC cân tại A)
BC là cạnh chung
=>tam giác BHC = tam giác CKB (c.g.c)
=>BH=CK (2 cạnh tương ứng) (dpcm)
Xét tam giác ABH và tam giác ACK ta có:
AB=AC (tam giác ABC cân tại A)
BH=CK (cmt)
AH=AK (gt)
=> tam giác ABH = tam giác ACK (c.c.c)
=> ABH = ACK (2 góc tương ứng) (dpcm)
b) Theo a) tam giác BHC= tam giác CKB
=> HBC=KCB (2 góc tương ứng) hay OBC=OCB
=> Tam giác OBC là tam giác cân tại O (dpcm)
c) Theo b tam giác OBC cân tại O => OB=OC
Theo a góc ABH = góc ACK => KBO= HCO
Xét tam giác OKB và tam giác OHC ta có:
KB=HC (theo a)
KBO=HCO (cmt)
OB=OC (cmt)
=> tam giác OKB = tam giác OHC (c.g.c)
=> OK = OH (2 cạnh tương ứng) hay tam giác OKH là tam giác cân tại O (dpcm)
d) Gọi giao điểm của AO và KH là I
Xét tam giác AKO và tam giác AHO ta có:
AK=AH (gt)
AO là cạnh chung
OK=OH (theo c)
=> tam giác AKO = tam giác AHO (c.c.c)
=> KAO = HAO (2 góc tương ứng) hay KAI=HAI
Xét tam giác KAI và tam giác HAI ta có:
AK=AH (gt)
KAI=HAI (cmt)
AI là cạnh chung
=> tam giác KAI = tam giác HAI ( c.g.c)
=> KI=HI , mà I nằm giữa H và K
=> I là trung điểm của KH hay
AO đi qua trung điểm của KH (dpcm)

Hình bn tự vẽ nha!!^^
a, Xét \(\Delta ADM\)VÀ \(\Delta ADN\)có:'
\(\widehat{MAD}=\widehat{DAN}\)(tia p/g \(\widehat{BAN}\))
\(AD\)chung
\(\widehat{ADN}=\widehat{ADM}\)(Đg thg \(\perp\))(=90 độ)
\(\Rightarrow\Delta'ADM=\Delta ADN\left(g.c.g\right)\)
\(\Rightarrow\widehat{M}=\widehat{N}\)(2 góc t/ứ)
Xét tam giác AMN có: \(\widehat{M}=\widehat{N}\Rightarrow\Delta AMN\)là tam giác cân tại A
Để chứng minh rằng \( BM = CN \), chúng ta sẽ sử dụng tính chất của tam giác cân.
Vì tam giác \( ABC \) cân tại \( A \), nên ta có \( AM = MC \) và \( AN = NB \), vì \( M \) là trung điểm của \( AC \) và \( N \) là trung điểm của \( AB \).
Bây giờ, ta cần chứng minh \( BM = CN \).
Ta có thể sử dụng định lí đối xứng của tam giác để chứng minh điều này.
Xét tam giác \( AMC \) và \( ANB \):
- \( AM = MC \) (vì \( M \) là trung điểm của \( AC \))
- \( AN = NB \) (vì \( N \) là trung điểm của \( AB \))
- \( AC = AB \) (vì tam giác \( ABC \) cân tại \( A \))
Theo định lí đối xứng của tam giác, ta có \( BM = CN \), vì hai tam giác \( AMC \) và \( ANB \) là đối xứng với nhau qua đường trung tuyến \( MN \).
Do đó, \( BM = CN \).
sai rồi