Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Xét ΔCDE vuông tại D và ΔCAB vuông tại A có
góc ACB chung
Do dó ΔCDE đồng dạng với ΔCAB
=>CD/CA=CE/CB
=>CD/CE=CA/CB
=>ΔCDA đồng dạng với ΔCEB
=>EB/DA=BC/AC
mà BC/AC=AC/CH
nên EB/DA=AC/CH=BA/HA
=>BE/AD=BA/HA
=>\(BE=\dfrac{AB}{AH}\cdot AD=\dfrac{AB}{AH}\cdot\sqrt{AH^2+HD^2}\)
\(=\dfrac{AB}{AH}\cdot\sqrt{AH^2+AH^2}=AB\sqrt{2}\)
b: Xét ΔABE vuông tại A có sin AEB=AB/BE=1/căn 2
nên góc AEB=45 độ
=>ΔABE vuông cân tại A
=>AM vuông góc với BE
BM*BE=BA^2
BH*BC=BA^2
Do đó: BM*BE=BH/BC
=>BM/BC=BH/BE
=>ΔBMH đồng dạng với ΔBCE

Xét ΔABC và ΔADE có
AB=AD
\(\widehat{BAC}\) chung
AC=AE
Do đó: ΔABC=ΔADE
Suy ra: \(\widehat{MCD}=\widehat{MEB}\)
Xét ΔCBE và ΔEDC có
CB=ED
CE chung
BE=DC
Do đó: ΔCBE=ΔEDC
Suy ra: \(\widehat{MBE}=\widehat{MDC}\)
Xét ΔMBE và ΔMDC có
\(\widehat{MBE}=\widehat{MDC}\)
BE=DC
\(\widehat{MEB}=\widehat{MCD}\)
Do đó: ΔMBE=ΔMDC
Suy ra: ME=MC
Xét ΔAME và ΔAMC có
AM chung
ME=MC
AE=AC
Do đó: ΔAME=ΔAMC
Suy ra: \(\widehat{EAM}=\widehat{CAM}\)
hay AM là tia phân giác của góc xAy

Chọn B.
Đặt AC = x > 0
Áp dụng định lí côsin trong tam giác ABD ta có
BD2 = 1 + (1 + x) 2 - 2.(1 + x). 1/x
Áp dụng định lí sin trong tam giác BCD ta có
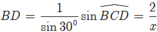
Suy ra ta được phương trình
![]()
Hay ![]() suy ra
suy ra ![]() (do x > 0).
(do x > 0).

Xét tứ giác ABEC có 2 đường chéo AE và BC cắt nhau tại trung điểm M của mỗi đường nên ABEC là hình bình hành
\(\Rightarrow\begin{cases}AB=CE\left(1\right)\\AB\backslash\backslash CE\end{cases}\)
a,xét ΔABM và ΔECM có:
\(\begin{cases}MA=ME\left(gt\right)\\MB=MC\left(gt\right)\\AB=CE\left(cmt\right)\end{cases}\)
→ΔABM=ΔECM(c.c.c)
b,Xét ΔABD có BH là đường cao đồng thời là đường trung tuyến
nên ΔABD cân tại B
→BC là phân giác của \(\widehat{ABD}\)
ΔABD cân tại B →AB=BD(2)
Từ (1),(2)→BD=CE

