Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Xét ΔBAM vuông tại A và ΔCAN vuông tại A có
BA=CA
\(\widehat{B}=\widehat{C}\)
Do đó: ΔBAM=ΔCAN
b: ΔBAM=ΔCAN
=>AM=AN và MB=CN
Ta có: ΔABC cân tại A
=>\(\widehat{ABC}=\widehat{ACB}=\dfrac{180^0-\widehat{BAC}}{2}=\dfrac{180^0-120^0}{2}=30^0\)
Ta có: \(\widehat{CAN}+\widehat{NAB}=\widehat{CAB}\)
=>\(\widehat{NAB}+90^0=120^0\)
=>\(\widehat{NAB}=30^0\)
ta có: \(\widehat{BAM}+\widehat{CAM}=120^0\)
=>\(\widehat{CAM}+90^0=120^0\)
=>\(\widehat{CAM}=30^0\)
Xét ΔNAB có \(\widehat{NAB}=\widehat{NBA}\left(=30^0\right)\)
nên ΔNAB cân tại N
Xét ΔMAC có \(\widehat{MAC}=\widehat{MCA}\left(=30^0\right)\)
nên ΔMAC cân tại M

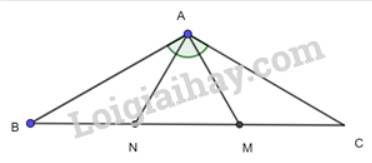
a) Xét 2 tam giác vuông BAM và CAN có:
\(\widehat{BAM} = \widehat{CAM}(=90^0)\)
AB=AC (Do tam giác ABC cân tại A)
\(\widehat B = \widehat C\) (Do tam giác ABC cân tại A)
=>\(\Delta BAM = \Delta CAN\)(g.c.g)
b) Cách 1:
Xét tam giác ABC cân tại A, có \(\widehat {A{\rm{ }}} = 120^\circ \) có:
\(\widehat B = \widehat C = \frac{{{{180}^o} - {{120}^o}}}{2} = {30^o}\).
Xét tam giác ABM vuông tại A có:
\(\widehat {B} + \widehat {BAM} + \widehat {AMB} = {180^o}\\ \Rightarrow {30^o} + {90^o} + \widehat {AMB} = {180^o}\\ \Rightarrow \widehat {AMB} = {60^o}\\ \Rightarrow \widehat {AMC} = {180^o} - \widehat {AMB} = {180^o} - {60^o} = {120^o}\)
Xét tam giác MAC có:
\(\begin{array}{l}\widehat {AMC} + \widehat {MAC} + \widehat C = {180^o}\\ \Rightarrow {120^o} + \widehat {MAC} + {30^o} = {180^o}\\ \Rightarrow \widehat {MAC} = {30^o} = \widehat C\end{array}\)
\(\Rightarrow \) Tam giác AMC cân tại M.
Vì \(\Delta BAM = \Delta CAN\)
=> BM=CN ( 2 cạnh tương ứng)
=> BM+MN=CN+NM
=> BN=CM
Xét 2 tam giác ANB và AMC có:
AB=AC (cmt)
\(AN = AM\)(do \(\Delta BAM = \Delta CAN\))
BN=MC (cmt)
=>\(\Delta ANB = \Delta AMC\)(c.c.c)
Mà tam giác AMC cân tại M.
=> Tam giác ANB cân tại N.
Cách 2:
Xét tam giác ABC cân tại A, có \(\widehat {A{\rm{ }}} = 120^\circ \) có:
\(\widehat B = \widehat C = \frac{{{{180}^o} - {{120}^o}}}{2} = {30^o}\).
Xét tam giác ABM vuông tại A có:
\(\widehat B + \widehat {BAM} + \widehat {AMB} = {180^o}\\ \Rightarrow {30^o} + {90^o} + \widehat {AMB} = {180^o}\\ \Rightarrow \widehat {AMB} = {60^o}\)
Vì \(\Delta BAM = \Delta CAN\) nên AM = AN (2 cạnh tương ứng)
=> \(\Delta AMN\) đều (Tam giác cân có 1 góc bằng 60 độ)
=> \(\widehat {NAM}=60^0\)
Ta có: \(\widehat{BAN}+\widehat{NAM}=\widehat{BAM}\)
=> \(\widehat{BAN} + 60^0=90^0\)
=> \(\widehat{BAN}=30^0\)
Xét tam giác ABN có \(\widehat{BAN}=\widehat{ABN}(=30^0\) nên \(\Delta ABN\) cân tại N.
Ta có: \(\widehat{CAM}+\widehat{NAM}=\widehat{CAN}\)
=> \(\widehat{CAM} + 60^0=90^0\)
=> \(\widehat{CAM}=30^0\)
Xét tam giác ACM có \(\widehat{CAM}=\widehat{ACM}(=30^0\) nên \(\Delta ACM\) cân tại M.

a: Xét ΔMHB vuông tại H và ΔNKC vuông tại K có
BM=CN
\(\widehat{B}=\widehat{C}\)
Do đó: ΔMHB=ΔNKC
b: Ta có: ΔMHB=ΔNKC
nên HB=KC
Ta có: AH+HB=AB
AK+KC=AC
mà BA=AC
và HB=KC
nên AH=AK
c: Xét ΔAHM vuông tại H và ΔAKN vuông tại K có
AH=AK
HM=KN
Do đó: ΔAHM=ΔAKN
Suy ra: AM=AN

bạn tự vẽ hình ạ
Xét tam giác BAM và tam giác MAN có:
BM=NM
góc BAM=góc NAm
AM:chung
suy ra:2 tam giác bằng nhau(C.G.C)
Suy ra góc BAM=gócMAN
Nhớ vote 5 sao nha

Đáp án đây nha
https://hoidapvietjack.com/q/648113/cho-abc-vuong-can-tai-a-goi-m-la-trung-diem-bc-d-la-diem-thuoc-doan-bm-d-khac-b-

a) Xét tam giác MBD vuông tại D và tam giác NCE vuông tại E có:
BM=CN(gt)
\(\widehat{B}=\widehat{C}\)(tam giác ABC cân)
Suy ra \(\Delta MBD=\Delta NCE\)(cạnh huyền-góc nhọn)
=>EC=BD(2 cạnh tương ứng)
b) Xét tam giác ADB và tam giác ACE có:
\(\widehat{B}=\widehat{C}\)(tam giác ABC cân)
AB=AC(tam giác ABC cân)
EC=BD(cmt)
Suy ra \(\Delta ADB=\Delta ACE\)(c.g.c)
=>AD=AE(2 cạnh tương ứng)
A B C M N D E
a, xét tam giác BDM và tam giác CEN có :
góc BDM = góc CEN = 90
BM = NC (Gt)
góc ABC = góc ACB do tam giác ABC cân tại A (Gt)
=> tam giác BDM = tam giác CEN (ch-gn)
b, tam giác BDM = tam giác CEN (câu a)
=> góc BMD = góc CNE (đn)
góc BMD + góc DMA = 180 (kb)
góc CNE + góc ENA = 180 (kb)
=> góc DMA = góc ENA (1)
có AB = AC do tam giác ABC cân tại A (gt)
BM = CN (gt)
BM + MA = AB
CN + NA = AC
=> MA = NA (2)
xét tam giác DMA và tam giác ENA có MD = EN do tam giác BDM = tam giác CEN (câu a)
(1)(2)
=> tam giác DMA = tam giác ENA (c-g-c)
=> AD = AE (đn)

a: Xét ΔBAM vuông tại A và ΔCAN vuông tại A có
BA=CA
góc B=góc C
=>ΔBAM=ΔCAN
b: ΔBAM=ΔCAN
=>AM=AN
góc MAB=90 độ
góc B=30 độ
=>góc AMN=60 độ
=>ΔAMN đều
góc NAB=120-90=30 độ=góc B
=>ΔNAB cân tại N
góc MAC=120-90=30 độ=góc C
=>ΔMAC cân tại M