K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên

18 tháng 2 2020
câu b là Vẽ BK vuông góc với AD sao cho K thuộc AD, CF vuông góc với AE sao cho CF thuộc AE nhé các bạn

H
25 tháng 7 2017
Theo mình nghĩ thì đề thiếu là tam giác ABC vuông tại A nhé!
Bạn xem lại đề!:)
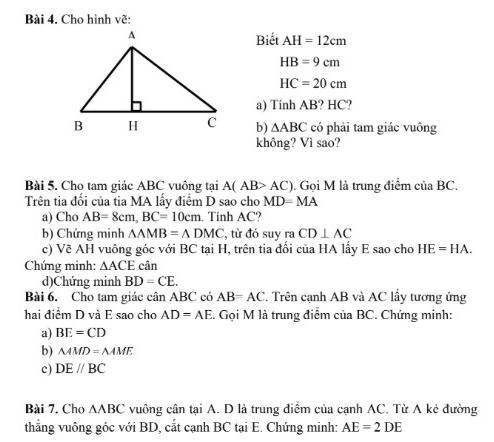
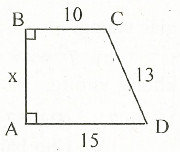
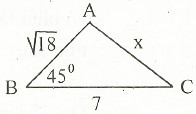
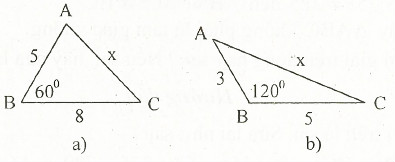
a: Xét ΔIHB vuông tại H và ΔIKC vuông tại K có
IB=IC
\(\widehat{B}=\widehat{C}\)
Do đó: ΔIHB=ΔIKC
b: Ta có: ΔIHB=ΔIKC
=>IB=IC
mà IC>IK(ΔIKC vuông tại K)
nên IB>IK
c:
Ta có: ΔIHB=ΔIKC
=>IH=IK
Xét ΔHIE vuông tại H và ΔKIF vuông tại K có
IH=IK
\(\widehat{HIE}=\widehat{KIF}\)(hai góc đối đỉnh)
Do đó; ΔHIE=ΔKIF
=>HE=KF
Ta có: AH+HB=AB
AK+KC=AC
mà HB=KC và AB=AC
nên AH=AK
Ta có: AH+HE=AE
AK+KF=AF
mà AH=AK và HE=KF
nên AE=AF
=>ΔAEF cân tại A
d: Xét ΔAEF có \(\dfrac{AH}{AE}=\dfrac{AK}{AF}\)
nên HK//EF