Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Câu 2:
Ta có: ΔABC vuông tại A
=>\(AB^2+AC^2=BC^2\)
=>\(BC^2=\left(2a\right)^2+\left(2a\sqrt{3}\right)^2=16a^2\)
=>BC=4a
Xét ΔABC vuông tại A có \(sinB=\dfrac{AC}{BC}=\dfrac{1}{2}\)
nên \(\widehat{ABC}=30^0\)
ΔABC vuông tại A
=>\(\widehat{ABC}+\widehat{ACB}=90^0\)
=>\(\widehat{ACB}=60^0\)
Lấy điểm E sao cho \(\overrightarrow{AB}=\overrightarrow{BE}\)
=>B là trung điểm của AE
=>\(\widehat{CBE}+\widehat{CBA}=180^0\)(hai góc kề bù)
=>\(\widehat{CBE}=180^0-30^0=150^0\)
\(\overrightarrow{AB}\cdot\overrightarrow{BC}=\overrightarrow{BE}\cdot\overrightarrow{BC}\)
\(=BE\cdot BC\cdot cos\left(\overrightarrow{BE};\overrightarrow{BC}\right)\)
\(=2a\sqrt{3}\cdot4a\cdot cos150=-12a^2\)
\(\left|\overrightarrow{AB}-\overrightarrow{AC}\right|=\left|\overrightarrow{AB}+\overrightarrow{CA}\right|=\left|\overrightarrow{CB}\right|=CB=4a\)

Áp dụng hệ thức đường trung tuyến m a 2 = b 2 + c 2 2 − a 2 4 ta được:
m a 2 = A C 2 + A B 2 2 − B C 2 4 = 12 2 + 9 2 2 − 15 2 4 = 225 4 .
⇒ m a = 15 2 .
Chọn A.

Chọn A.
Áp dụng hệ thức đường trung tuyến ![]() ta được:
ta được:
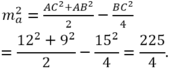
Suy ra : ma= 7,5.

\(tanB=\dfrac{AC}{AB}=\sqrt{3}\Rightarrow B=60^0\)
\(\Rightarrow\widehat{BAM}=\widehat{B}=60^0\)
\(AM=\dfrac{1}{2}BC=\dfrac{1}{2}\sqrt{AB^2+AC^2}=a\)
\(\overrightarrow{BA}.\overrightarrow{AM}=-\overrightarrow{AB}.\overrightarrow{AM}=-AB.AM.cos\widehat{BAM}=-\dfrac{a^2}{2}\)

Gọi G là giao điểm của AM và BN.
Theo công thức tính độ dài đường trung tuyến: \(AM^2=\dfrac{2b^2+2c^2-a^2}{4}\);
\(BN^2=\dfrac{2c^2+2a^2-b^2}{4}\).
Từ đó \(AG^2=\dfrac{4}{9}AM^2=\dfrac{2b^2+2c^2-a^2}{9}\); \(BG^2=\dfrac{4}{9}BN^2=\dfrac{2c^2+2a^2-b^2}{9}\).
Do đó \(AG^2+BG^2=\dfrac{a^2+b^2+4c^2}{9}=\dfrac{9c^2}{9}=c^2=AB^2\).
Theo định lý Pythagoras đảo thì tam giác AGB vuông tại G.
Vậy góc giữa 2 trung tuyến AM và BN là 90o.

Lời giải:
Vì AMAM là trung tuyến nên MM là trung điểm của BCBC
⇒−−→BM+−−→CM=→0⇒BM→+CM→=0→ (hai vecto đối nhau)
Ta có:
2−−→AM=(−−→AB+−−→BM)+(−−→AC+−−→CM)2AM→=(AB→+BM→)+(AC→+CM→)=−−→AB+−−→AC+(−−→BM+−−→CM)=AB→+AC→+(BM→+CM→)
=−−→AB+−−→AC=AB→+AC→
⇒−−→AM=12−−→AB+\(\frac{1}{2}\)−−→AC

\(AM=\sqrt{\dfrac{4.2^2+6.5^2}{2}-\dfrac{7.2^2}{4}}\simeq4,12\left(cm\right)\)
BM=BC/2=3,6cm
Xét ΔBAM có BI là phân giác
nên IA/AB=IM/BM
=>IA/42=IM/36
=>IA/7=IM/6=(IA+IM)/(7+6)=AM/13=4,12/13
=>\(IA\simeq2,22\left(cm\right);IM\simeq1,9\left(cm\right)\)
AM là trung tuyến của tam giác ABC cân tại A
=> AM là đường trung trực của tam giác ABC
=> M là trung điểm của BC
=> \(BM=CM=\frac{BC}{2}=\frac{32}{2}=16\) (cm)
Tam giác ABM vuông tại M có:
\(AB^2=AM^2+BM^2\)
\(34^2=AM^2+16^2\)
\(AM^2=34^2-16^2\)
\(AM^2=1156-256\)
\(AM^2=900\)
\(AM=\sqrt{900}\)
\(AM=30\) (cm)
Chúc bạn học tốt
Tớ làm thế này có đúng ko nhé
Vì đường trung tuyến đi qua trung điểm của
đoạn thẳng BC
Suy ra: BM=CM=32:2=16cm
Xét tam giác ABM và AMC
AB=AC(gt)
AM là cạnh chung
MB=MC(gt)
⇒tam giác ABM=tam giác AMC(c.c.c)
Do đó góc AMB=góc AMC(1)
Mà góc AMB+gócAMC=180(kề bù)(2)
Từ 1 và 2 suy ra góc AMB= góc AMC=90 độ
Xét tam giác ABM vuông tại M
Áp dụng định lý Pi-Ta-Go ta có
AM2+BM2=AB2
AM2+162=342
AM=342-162=900
AM=30
vậy AM=30 cm