K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên

CM
15 tháng 9 2017
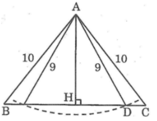
Kẻ AH ⊥ AB.
Xét hai tam giác vuông AHB và AHC, ta có:
∠AHB = ∠AHC = 90o
AB = AC (gt)
AH cạnh chung
Suy ra: ΔAHB = ΔAHC
(cạnh huyền - cạnh góc vuông)
Suy ra: HB = HC (hai cạnh tương ứng)
Ta có: HB = HC = BC/2 = 6 (cm)
Trong tam giác vuông AHB có ∠AHB = 90o
Áp dụng định lí Pi-ta-go, ta có:
AB2 = AH2 + HB2 ⇒ AH2 = AB2 – HB2 = 102 – 62 = 64
⇒ AH = 8 (cm)
Do bán kính cung tròn 9(cm) > 8(cm) nên cung tròn tâm A bán kính 9 cm cắt đường thẳng BC.
Gọi D là giao điểm của cung tròn tâm A bán kính 9 cm với BC.
Vì đường xiên AD < AC nên hình chiếu HD < HC.
Do đó D nằm giữa H và C.
Vậy cung tròn tâm A bán kính 9 cm cắt cạnh BC.
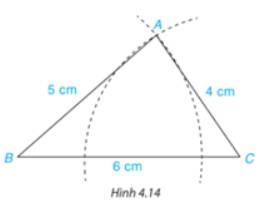


Kẻ AH vuông góc với BC
Xét ΔAHB vuông tại H và ΔAHC vuông tại H có
AB=AC
AH chung
Do đó; ΔAHB=ΔAHC
Suy ra: HB=HC=BC/2=6(cm)
=>AH=8(cm)
Vì R=9cm nên cung tròn này cắt đường thẳng CB
Gọi D là giao điểm của (A;9cm) với BC
Vì AD<AC nên HD<HC
=>D nằm giữa H và C
hay cung tròn này cắt cạnh BC