Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

xét tam giác ABD và tam giác ACD có:
AB=AC
AD(chung)
BAD=CAD(gt)
suy ra tam giác ABD=ACD(c.g.c)
suy ra _ADB=ADC mà ADC+ADB=180 suy ra ADC=ADB=180/2=90
|
-DB=DC=1/2BC=5cm
vì AD là 1 đường trung tuyến của tam giác ABC, G là trọng tâm của tam giác ABC suy ra GD=1/3AD
ta có:\(AD^2=AB^2-BD^2=13^2-5^2=169-25=144\)
\(AD=\sqrt{144}=12\left(cm\right)\)
GD=1/3AD=1/3x12=4(cm)
Cho tam giác ABC cân tại A,AH phân giác G là trọng tâm của ABC.tính AG, GH,AH? Biết AB=8cm, BC =12cm


nhìn vào hình vẽ nhá, tớ gửi hình trước cho cậu dễ thấy thôi:
a) xét 2 tam giác vuông: ABH VÀ ACH, CÓ:
AH LÀ CẠNH CHUNG
AB = AC (VÌ TAM GIÁC ABC CÂN TẠI A)
=> \(\Delta ABH=\Delta ACH\) (CẠNH HUYỀN - CẠNH GÓC VUÔNG)
a) Xét tam giác ABH và tam giác ACH
có AB = AC
AH cạnh chung
\(\Rightarrow\)tam giác ABH = tam giác ACH

Bạn tự vẽ hình nha!
a.
Xét tam giác ABM và tam giác ACM có:
AB = AC (tam giác ABC cân tại A)
B = C (tam giác ABC cân tại A)
BM = CM (AM là trung tuyến của tam giác ABC)
=> Tam giác ABM = Tam giác ACM (c.g.c)
b.
Tam giác ABM = Tam giác ACM (theo câu a)
=> M1 = M2 (2 góc tương ứng)
mà M1 + M2 = 180 (2 góc kề bù)
=> M1 = M2 = 180/2 = 90
=> AM _I_ BC
( Cái này bạn chứng minh theo cách: AM là trung tuyến của tam giác ABC cân tại A nên AM là đường trung trực của tam giác ABC cũng được. Tại mình sợ bạn chưa học tới)
BM = CM = BC/2 (AM là trung tuyến của tam giác ABC)
=> BM = CM = 10/2 = 5
Áp dụng định lí Pytago vào tam giác ABM vuông tại A ta có:
AB^2 = BM^2 + AM^2
13^2 = 5^2 + AM^2
AM^2 = 169 - 25
AM = 12
Ta có: AG = 2/3 AM (tính chất trọng tâm)
=> AG = 2/3 . 12
AG = 8
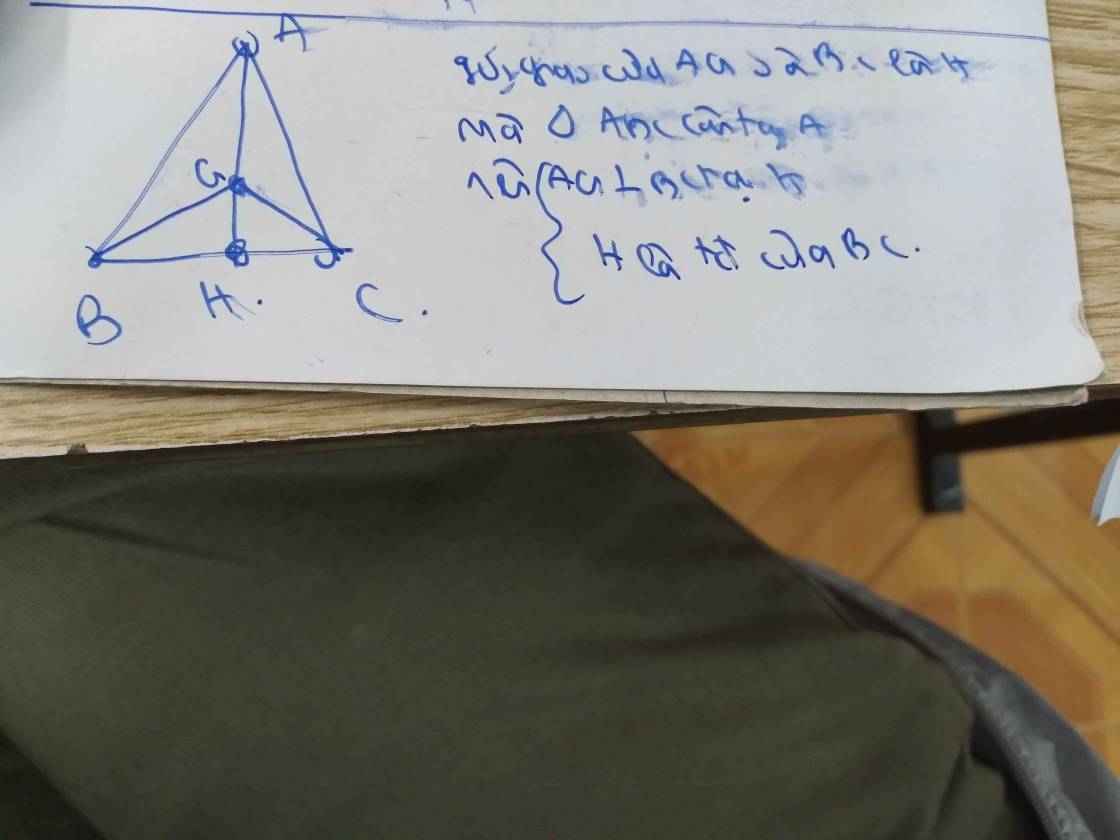

Vì AH là đường Phân giác của \(\Delta ABC\)cân tại A
\(\Rightarrow\)AH là đường cao cửa tam giác cân ABC
\(\Rightarrow AH\perp BC\equiv H\)\(\Rightarrow\Delta AHB\)vuuoong tại H
Ta có Đường phân giác AH đi qua trọng tâm G
\(\Rightarrow\)AH là trung tuyến của \(\Delta ABC\) đi qua BC
\(\Rightarrow\)HB=HC
Mà HB+HC=BC
\(\Rightarrow\)\(HB=HC=\frac{BC}{2}\)\(=\frac{16}{2}=4\)
Ta có: \(AB^2=AH^2+HB^2\)(áp dụng định lý pyta go cho tam giác AHB vuông tại H)
\(\Rightarrow10^2=AH^2+4^2\)
\(\Rightarrow AH^2=10^2-4^2\)\(=84\)
\(\Rightarrow\sqrt{84}\)
Mà G là trọng tâm của tam giác ABC
\(\Rightarrow AG=\frac{2}{3}AH\)
còn lại tự tính nha ta hướng dẫn là rồi đó
có một số chỗ ta nhầm bỏ từ chỗ \(HB=HC=\frac{BC}{2}=\frac{16}{2}\)\(=4\)
sửa lại :\(HB=HC=\frac{BC}{2}=\frac{16}{2}\)\(=8\)
\(AB^2=AH^2+HB^2\)(áp dụng định lý pytago cho \(\Delta AHB\)vuông tại A)
\(\Rightarrow10^2=AH^2+8^2\)
\(\Rightarrow AH^2=10^2-8^2=36\)
\(\Rightarrow AH=6\)
Mà G là trọng tâm của \(\Delta ABC\)
\(\Rightarrow AG=\frac{2}{3}AH\)
hay \(AG=\frac{2}{3}.6\)
\(\Rightarrow AG=4cm\)
vậy AG=4cm