Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Chọn đáp án B
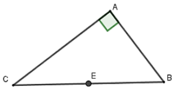
Vì tam giác ABC vuông tại A nên tâm đường tròn ngoại tiếp là trung điểm cạnh huyền BC, bán kính là R = BC/2
Theo định lý Pytago ta có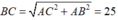 
nên bán kính R = 25/2
Kẽ OA cắt đường tròn tại D cắt BC tại K
Ta có OA = OB = OD = R
\(\Rightarrow\)\(\Delta ABD\) vuông tại D
\(\Rightarrow BD=\sqrt{OD^2-AB^2}=\sqrt{10^2-8^2}=6\)
Ta có OK là đường trung trực của BC nên \(\hept{\begin{cases}OK⊥BC\\BK=CK\end{cases}}\)
Ta lại có: \(S_{\Delta ABD}=\frac{1}{2}AB.BD=\frac{1}{2}AD.BK\)
\(\Rightarrow BK=\frac{AB.BD}{AD}=\frac{8.6}{10}=4,8\)
\(\Rightarrow BC=2BK=4,8.2=9,6\)
Viết nhầm tùm lum hết. Do không thấy cái hình. Mà thôi nhìn hình sửa hộ luôn nhé
Kéo dài đường cao AH cắt đường tròn ngoại tiếp tam giác ABC tại D . Gọi O là tâm đường tròn ngoại tiếp tam giác ABC
Vì tam giác ABC cân tại A nên AHlà đường trung trực của BC . Nên AD là đường trung trực của BC .
Khi đó O thuộc AD hay AD là đường kính của đường tròn ngoại tiếp tam giác ABC
Tam giác ACD nội tiếp trong (O ) có AD là đường khính suy ra \(\widehat{ACD=90}\)độ
Tam giác ACD vuông tại C nên theo hệ thức liên hệ giữa đường cao và hình chiếu , ta có :
\(CH^2=HA.HD\)
\(\Rightarrow\)\(HD=\frac{CH^2}{HA}=\frac{\left(\frac{BC}{2}\right)^2}{HA}=\frac{\left(\frac{12}{2}^2\right)}{4}=\frac{6^2}{4}=9cm\)
Ta có \(AD=AH+HD=4+9=13\left(cm\right)\)
Vậy bán kính của đường tròn (O ) là :
\(R=\frac{AD}{2}=\frac{13}{2}=6,5\left(cm\right)\)
Chúc bạn học tốt !!!
(Hình)
Diện tích tam giác ABC là:
SABC = 1/2 . AH . BC = 1/2 . 4 . 12 = 24 (cm2)
Vì tam giác ABC cân tại A nên đường cao AH là trung tuyến BC
Nên : BH= HC= 1/2. BC= 1/2 . 12 = 6 (cm)
Trong tam giác AHB:
Áp dụng ĐL pi-ta-go:
AB2 = AH2 + BH2
AB2 = 42 + 62
AB= \(2\sqrt{13}\) (cm)
Vì tam giác ABC cân tại A nên : AB = AC = \(2\sqrt{13}\) (cm)
Ta có : SABC =\(\frac{AB\cdot AC\cdot BC}{4R}\) (R là bán kính đường tòn ngoại tiếp tam giác ABC)
<=> \(24=\frac{2\sqrt{13}.2\sqrt{13}.12}{4R}\)
<=> R= \(\frac{13}{2}\) (cm)
OK