
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Kẻ đg cao AH thì AH cũng là trung tuyến
Do đó \(BH=\dfrac{1}{2}BC=5\left(cm\right)\)
\(\Rightarrow\cos\widehat{B}=\dfrac{BH}{AB}=\dfrac{5}{13}\)

\(AB^2=AH.BC\Rightarrow BC=\frac{AB^2}{AH}=\frac{7,5^2}{6}=9,375\)
áp dụng định lí Pytago tính được AC = 5,625
tính cosB và cos C thì quá dễ rồi. bạn làm tiếp nhé

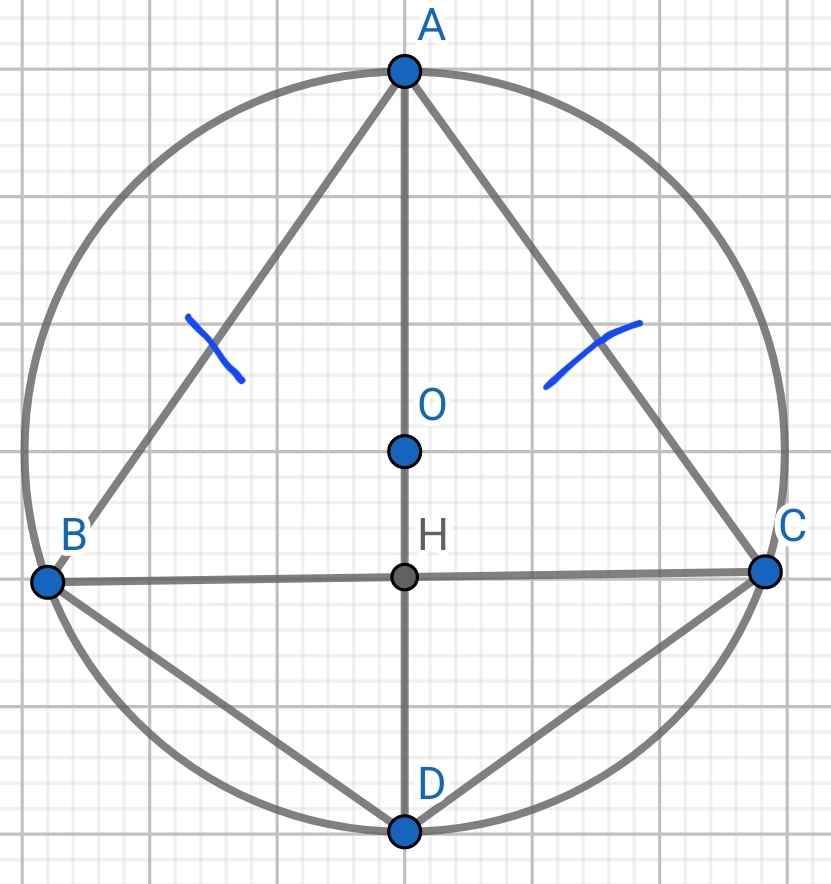
Do (O) là đường tròn ngoại tiếp ∆ABC
⇒ O là giao điểm của ba đường trung trực của ∆ABC
⇒ AO là đường trung trực của ∆ABC
⇒ AO ⊥ BC tại H
⇒ H là trung điểm BC
⇒ BH = BC : 2 = 12 : 2 = 6 (cm)
Do ∠ABD là góc nội tiếp chắn nửa đường tròn
⇒ ∠ABD = 90⁰
∆ABD vuông tại B có BH là đường cao
⇒ 1/BH² = 1/AB² + 1/BD²
⇒ 1/BD² = 1/BH² - 1/AB²
= 1/36 - 1/100
= 4/225
⇒ BD² = 225/4
⇒ BD = 15/2 = 7,5 (cm)
∆ABD vuông tại B
⇒ AD² = AB² + BD² (Pytago)
= 10² + 7,5²
= 156,25
⇒ AD = 12,5 (cm)
Để tính độ dài đoạn thẳng AD, ta cần tìm được tọa độ của điểm D trên đường tròn (O).
Gọi M là trung điểm của đoạn BC. Ta có AM là đường trung trực của BC, do đó OM vuông góc với BC và OM = MC = 6(cm).
Vì tam giác ABC cân tại A nên đường trung trực của BC cũng là đường cao của tam giác. Do đó, ta có AH là đường cao của tam giác ABC và AH = $\sqrt{AB^2 - BM^2}$ = $\sqrt{100 - 36}$ = $\sqrt{64}$ = 8(cm).
Ta có thể tính được AO bằng định lý Pythagoras trong tam giác vuông AOM:
$AO^2 = AM^2 + OM^2 = 10^2 - 6^2 + 6^2 = 100$
Vậy $AO = 10$ (cm).
Do đó, ta có thể tính được bán kính đường tròn (O) là $R = \frac{BC}{2} = 6$ (cm).
Gọi E là điểm đối xứng của A qua đường tròn (O). Ta có AE là đường đối xứng của AH qua đường tròn (O), do đó AE = AH = 8 (cm).
Ta có thể tính được độ dài đoạn thẳng DE bằng định lý Pythagoras trong tam giác vuông AOD:
$DE^2 = DO^2 + OE^2 = R^2 + AE^2 = 6^2 + 8^2 = 100$
Vậy $DE = 10$ (cm).
Ta cần tính độ dài đoạn thẳng AD. Ta có thể tính được độ dài đoạn thẳng HD bằng định lý Euclid:
$\frac{HD}{BD} = \frac{AH}{AB}$
$\Rightarrow HD = \frac{AH \cdot BD}{AB} = \frac{8 \cdot 6}{10} = \frac{24}{5}$ (cm)
Ta có thể tính được độ dài đoạn thẳng AO bằng định lý Pythagoras trong tam giác vuông AHO:
$AD^2 = AO^2 + OD^2 - 2 \cdot AO \cdot OD \cdot \cos{\angle AOD}$
Vì tam giác AOD cân tại O nên $\angle AOD = \frac{1}{2} \cdot \angle AOB$. Ta có thể tính được $\angle AOB$ bằng định lý cosin trong tam giác ABC:
$\cos{\angle AOB} = \frac{AB^2 + AC^2 - BC^2}{2 \cdot AB \cdot AC

kẽ đường cao AH,tam giác ABC cân tại A=>AH cũng là trung tuyến của BC=>BH=1/2BC=5cm
xét tam giác AHB theo DL Pitago ta tính dc AH=12cm
=>cosBAH=AH/AB=12/13
=>cosBAC=2*12/13=24/13(vì AH là fân giác góc BAC)

Tính AB bằng hệ thức đường cao trong tam giác vuông. 1/h^2=1/a^2+ 1/b^2 .
Tính BC dùng pytago. sau khi tìm AB
Tính cos B = AB/BC, cosC = AC/BC

Câu 1: Tam giác ABC vuông tại A có AM là đường trung tuyến ứng với cạnh huyền BC
=> AM=\(\frac{1}{2}\)BC mà AM=6 cm=> BC=12cm.
Tam giác ANB vuông tại A có AN2+AB2=BN2 (Theo Pytago) mà BN=9cm (gt)
=>AN2+AB2=81 Lại có AN=\(\frac{1}{2}\)AC =>\(\frac{1}{2}\)AC2+AB2=81 (1)
Tam giác ABC vuông tại A có: AC2+AB2=BC2 => BC2 - AB2 = AC2 (2)
Từ (1) và (2) suy ra \(\frac{1}{4}\)* (BC2 - AB2)+AB2=81 mà BC=12(cmt)
=> 36 - \(\frac{1}{4}\)AB2+AB2=81
=> 36+\(\frac{3}{4}\)AB2=81
=> AB2=60=>AB=\(\sqrt{60}\)
C2
Cho hình thang cân ABCD có đáy lớn CD = 1
C4
Câu hỏi của Thiên An - Toán lớp 9 - Học toán với OnlineMath
Kẻ AH vuông góc với BC.
Vì ABC là tam giác cân nên AH là trung tuyến ứng với BC.
=> HB = HC = BC/2 = 10/2=5 cm.
cos C = 5/13 => Góc C = 67 độ 38 phút.
Vì ABC là tam giác cân nên góc B = Góc C = 67 độ 23 phút.
=> Góc A = 180 - 2 . 67 độ 23 phút = 45 độ 14 phút
=> cos A = 119/169
(Mik ko có kẻ hình đâu nha)