Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Bài 1 : Hình tự vẽ
a ) Ta có : BM = AB ( theo đề bài )
=> Tam giác AMB cân tại B
b ) Do tam giác ABC vuông cân tại A => AB = AC
mà CN = AB => CN cũng = AC
=> Tam giác ANC cân tại C
c ) Tam giác j cân tại A ???
Bài 2 : Hình bn tự vẽ nhé
a ) AH \(\perp\)BC => \(\Delta AHB\)và \(\Delta AHC\)là hai tam giác vuông
Do tam giác ABC cân tại A => AB = AC và \(\widehat{ABC}=\widehat{ACB}\)
Xét hai tam giác vuông : \(\Delta AHB\)và \(\Delta AHC\)có :
AB = AC ( cmt )
\(\widehat{ABC}=\widehat{ACB}\)( cmt )
nên tam giác AHB = tam giác AHC ( cạnh huyền - góc nhọn )
b ) Do tam giác AHB = tam giác AHC => HB = HC ( hai cạnh tương ứng )
c ) Do tam giác AHB = tam giác AHC => \(\widehat{BAH}=\widehat{CAH}\)
=> AH là tia p/g của \(\widehat{BAC}\)

a, Xét tam giác vuông ABH và tam giác vuông ACH có:
AB = AC ( tam giác ABC cân ở A)
AH chung
=> tam giác vuông ABH = tam giác vuông ẠCH (ch - cgv)
=> HC = HB ( cạnh tương ứng )
b, Từ câu a => góc BAH = góc CAH (góc tương ứng)
=> AH là phân giác góc BAC
a) Vì AH \(⊥\)BC \(\Rightarrow\)\(\Delta\)AHB và \(\Delta\)AHC là\(\Delta\)vuông tại H.
Xét \(\Delta\)AHB và \(\Delta\)AHC,có :
AB =AC( \(\Delta\)ABC cân tại A)
\(\widehat{B}=\widehat{C}\)( \(\Delta ABC\)cân tại A)
Vậy \(\Delta\)vuông AHB =\(\Delta\)vuông AHC (Cạnh huyền - góc nhọn )
\(\Rightarrow HB=HC\)( 2 cạnh tương ứng)
b) Vì \(\Delta ABH=\Delta AHC\left(cmt\right)\)
\(\widehat{A}\)1 =\(\widehat{A}\)2 (2 góc tương ứng)
Vậy AH là tia phân giác của \(\widehat{BAC}\)

a) xét tg AMC và tg ABN có
MA=BA(gt)
CA=AN(gt)
ˆMAC=ˆBAN(doˆMAB+ˆBAC=ˆNAC+ˆBAC)MAC^=BAN^(doMAB^+BAC^=NAC^+BAC^)
=>(kết luận)...
b)gọi I là giao điểm của MC và BN
gọi giao điểm của BA và MI là F
vì ΔAMC=ΔABNΔAMC=ΔABNnên
ˆFMA=ˆFBIFMA^=FBI^
mà ˆFMA+ˆFMB=45OFMA^+FMB^=45O
=>ˆFBI+ˆIMB=45OFBI^+IMB^=45O
Xét ΔIMBΔIMBcó góc ˆIMB+ˆMBI+ˆBIMIMB^+MBI^+BIM^= 180O
Mà ˆIMB+ˆMBIIMB^+MBI^=900
=>...
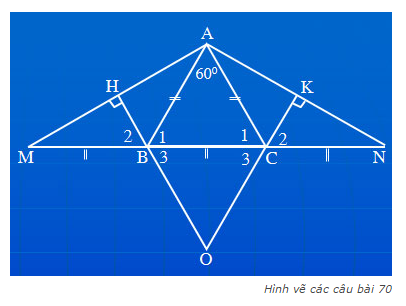
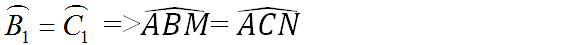
Ta có hình vẽ:
ABCH
Ta có: AC = AB và góc CAH = BAH (tính chất của Δ cân)
Cách 1: Xét Δ AHB và Δ AHC có:
AB = AC (gt)
BAH = CAH (chứng minh trên)
AH là cạnh chung
Do đó, Δ AHB = Δ AHC (c.g.c) (đpcm)
Cách 2: Vì AH⊥BC⇒AHC=AHB=90oAH⊥BC⇒AHC=AHB=90o
Xét Δ AHB và Δ AHC có:
CAH = BAH (chứng minh trên)
AB = AC (gt)
AHC = AHB (chứng minh trên)
Do đó, Δ AHB = Δ AHC (g.c.g) (đpcm)
bạn ơi cái này là tam giác vuông mà