Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
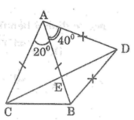
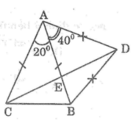
a) Theo giả thiết, =
=
.60o = 30o
=
+
(tia CB nằm giữa hai tia CA, CD)
=> = 60o + 30o = 90o (1)
Do DB = CD nên ∆BDC cân => =
= 30o
Từ đó = 60o + 30o = 90o (2)
Từ (1) và (2) có +
= 180o nên tứ giác ABDC nội tiếp được.
b) Vì = 90o nên AD là đường kính của đường tròn ngoại tiếp tứ giác ABDC, do đó tâm đường tròn ngoại tiếp tứ giác ABDC là trung điểm AD.
DC = DA
OA = OC
Do đó OD là trung trực của đoạn thẳng AC : suy ra OD vuông góc với AC
Tứ giác OECH có góc CEO + góc CHO = 180 độ
Suy ra tứ giác OECH là tứ giác nội tiếp
Do tam giác ABC là tam giác nên A C B ^ = 60 o
=> Tứ giác ABDC có: 
=> ABDC là tứ giác nội tiếp