Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Xét △AMB và △ANC ta có:
AM=AN ( Vì M,N lần lượt là trung điểm của 2 cạnh AB, AC)
\(\widehat{A}\) là góc chung
AB=AC (Vì là hai cạnh bên trong tam giác cân)
\(\Rightarrow\Delta AMB=\Delta ANC\left(c-g-c\right)\)
\(\Rightarrow BM=CN\) (hai cạnh tương ứng)
Xét ΔAMB và ΔANC có
AM=AN
góc A chug
AB=AC
=>ΔAMB=ΔANC
=>BM=CN

Tham khảo:
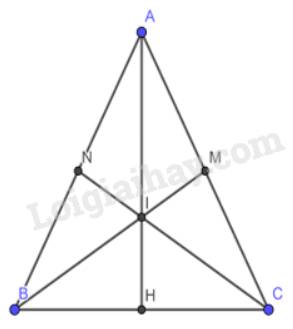
a) Vì tam giác ABC cân tại A theo giả thiết. BM và CN là 2 đường trung tuyến nên M, N là 2 trung điểm của AC, AB.
Vì AB = AC (tính chất tam giác cân)
\( \Rightarrow \dfrac{{AB}}{2} = \dfrac{{AC}}{2} = AN = AM\)
Xét tam giác AMB và tam giác ANC ta có :
AM = AN (cmt)
AB = AC
Góc A chung
\( \Rightarrow \Delta AMB =\Delta ANC\)
\( \Rightarrow BM = CN\) ( 2 cạnh tương ứng )
b) Vì BM và CN là các đường trung tuyến
Mà I là giao điểm của BM và CN
\( \Rightarrow \) I là trọng tâm của tam giác ABC
\( \Rightarrow \) AI là đường trung tuyến của tam giác ABC hay AH đường là trung tuyến của tam giác ABC
\( \Rightarrow \) H là trung điểm của BC

vì tgiac ABC cân tại A
có BM và CN là trung tuyến=> AM=MC=AN=NB
a, xét tgiac BMC và tgiac CNB có:
BC là cạnh chung
góc B= góc C(gt)
BM=CN(cmt)
vậy tgiac BMC=Tgiac CNB(c.g.c)
b. xét tgiac AMN có AM=AN(cmt)
=> tgiac AMN cân tại đỉnh A
ta lại có tgiac ABC cân tại A
Vậy góc ANM= góc ABC= (180-góc A):2
mà góc ANM và góc ABC ở vị trí đồng vị => MN//BC
c.ta có BM cắt CN tại G=> G là trọng tâm tgiac ABC=> AG là đường trung tuyến ứng vơi cạnh BC
mà tamgiac ABC cân tại A nên đường trung tuyến AG cũng là đường cao vậy AG vuông góc với BC
mà BC//MN nên AG vuông góc với MN(từ vuông góc đến //)

a: Xet ΔAHB và ΔAHC có
AH chung
HB=HC
AB=AC
=>ΔAHB=ΔAHC
b: Xét ΔNBC và ΔMCB có
NB=MC
góc NBC=góc MCB
CB chung
=>ΔNBC=ΔMCB
=>góc GBC=góc GCB
=>ΔGCB cân tại G
c: góc ECG+góc BCG=90 độ
góc GBC+góc GEC=90 độ
mà góc BCG=góc GBC
nên góc ECG=góc GEC
=>GC=GE=GB
=>G là trung điểm của BE
Xét ΔEBC có GD//CB
nên GD/CB=EG/EB=1/2
=>CB=2GD

a: Xét ΔBNC và ΔCMB có
NB=MC
\(\widehat{NBC}=\widehat{MCB}\)
BC chung
Do đó; ΔBNC=ΔCMB
b: Sửa đề: Cm ΔANM cân tại A
Xét ΔANM có AN=AM
nên ΔANM cân tại A

Xét ΔABM và ΔACN có
AB=AC
góc BAM chung
AM=AN
=>ΔABM=ΔACN
=>BM=CN
Mình xin phép sửa đề:
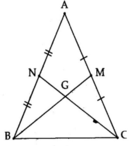
Cho tam giác ABC cân tại A , các đường trung tuyến BM và CN cắt nhau tại G
Chứng minh tam giác ABN = tam giác ACN , từ đó suy ra BM=CN
`------`
\(\text{GT | AB = AC, }\widehat{\text{B}}=\widehat{\text{C}}\)
\(\text{CM | BM = CN}\)
\(\text{BM là đường trung tuyến}\)
`->`\(\text{MA = MC (1)}\)
\(\text{CN là đường trung tuyến}\)
`->`\(\text{NA = NB (2)}\)
`\Delta ABC` cân tại A
`->`\(\widehat{\text{B}}=\widehat{\text{C}}\text{, AB = AC (3)}\)
Từ \(\left(1\right),\left(2\right),\left(3\right)\)
`->`\(\text{NA = NB = MA = MC}\)
Xét `\Delta ABM` và `\Delta ACN`:
\(\left\{{}\begin{matrix}\text{BM = CN}\\\widehat{\text{B}}=\widehat{\text{C}}\\\text{BC chung}\end{matrix}\right.\)
`=> \Delta ABM = \Delta ACN (c-g-c)`
`->`\(\text{BM = CN (2 cạnh tương ứng).}\)