Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

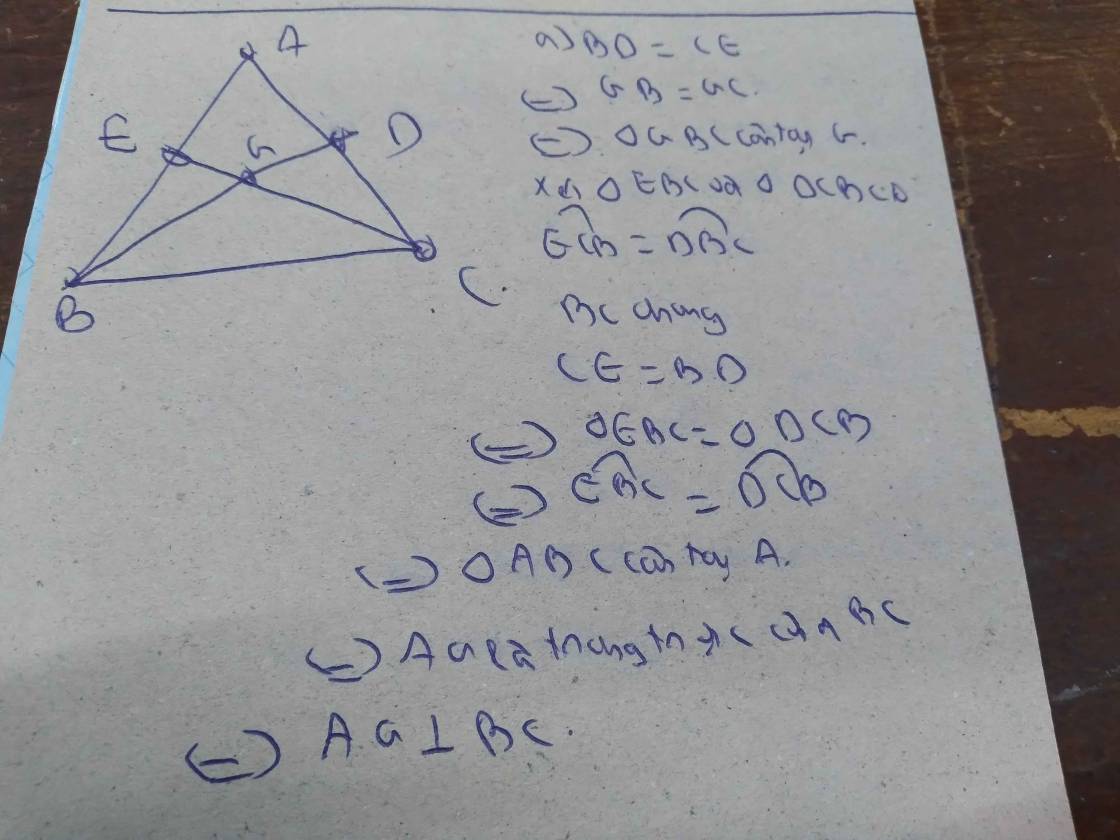
Xét tgiac ACE. ADB:
góc A chung
D=E=90¤
AB=AC
=> Tgiac ACE==ABD (c-h-g-n)
=> BD=CE ( 2ctu) và AE=AD ( sử dụng cho cậu c))
b) BD giao CE tại G=> G là trực tâm tgiac ABC
=> AG vuông góc với BC
c) Xét 2 t giác AEG=ADG ( c-h-c-g-v)
=>GE=GD(2ctu) =>GB=GC=> tgiac GBC cân tại B

xét ΔECB và ΔDBC, ta có :
EC = BD (gt)
\(\widehat{B}=\widehat{C}\) (2 góc đáy của ΔABC cân tại A)
BC là cạnh chung
=> ΔECB = ΔDBC (c.g.c)
=> \(\widehat{GBC}=\widehat{GCB}\) (2 góc tương ứng)
vì ΔGBC có \(\widehat{GBC}=\widehat{GCB}\) nên ⇒ ΔGBC là một tam giác cân (cân tại G)

Ta có: \(BD< CE\left(gt\right)\)
=> \(\frac{2}{3}BD< \frac{2}{3}CE\) (tính chất trọng tâm của tam giác)
Hay \(BG< CG.\)
Trong \(\Delta BDC\) có \(\widehat{GBC}\) đối diện với cạnh \(GC;\widehat{GCB}\) đối diện với cạnh \(GB.\)
Mà \(GB< GC\left(cmt\right)\)
=> \(\widehat{GCB}< \widehat{GBC}\) (theo quan hệ giữa góc và cạnh đối điện trong tam giác)
Chúc bạn học tốt!


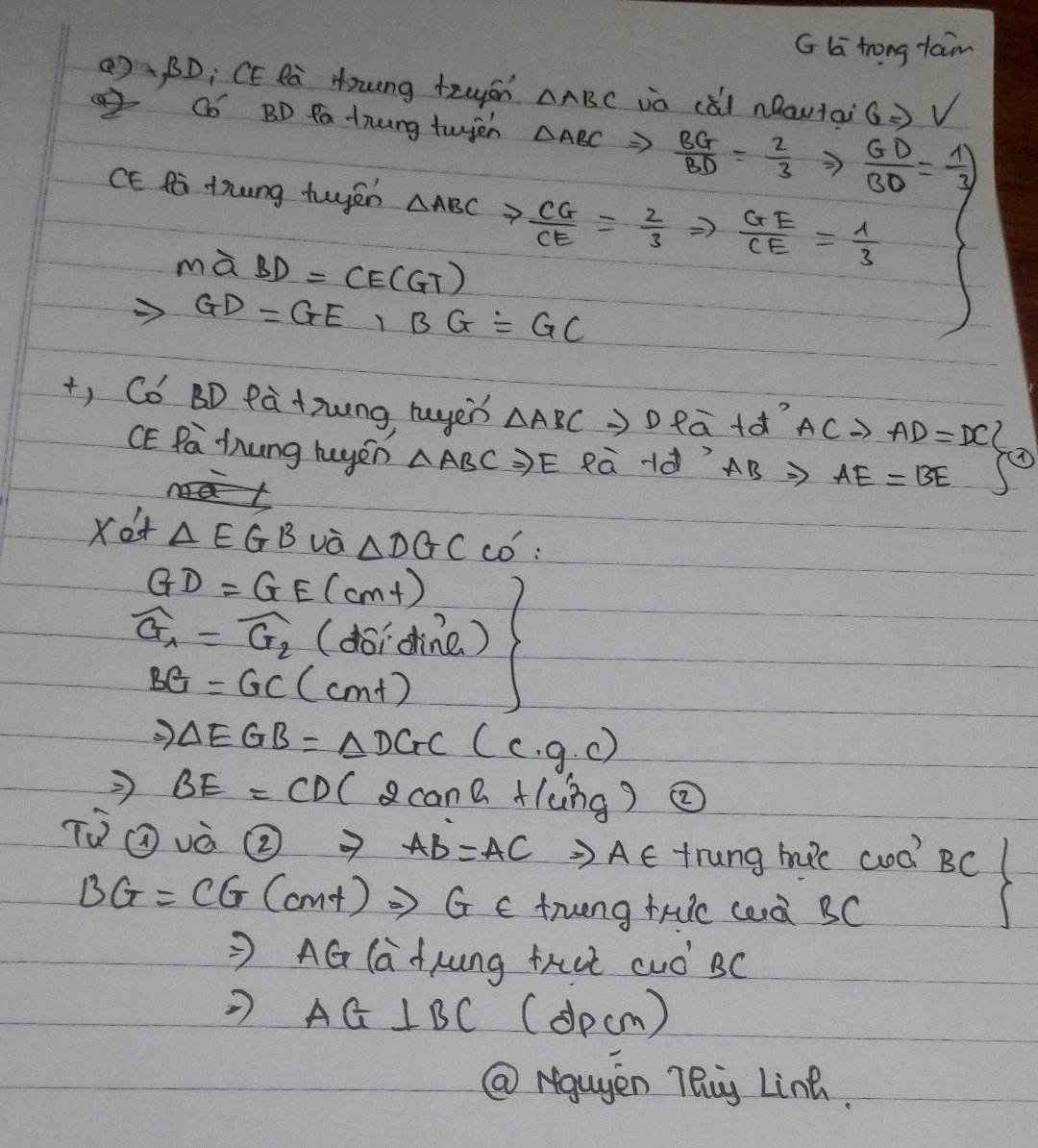

BD < CE => 2/3 . BD < 2/3 . CE (tính chất trọng tâm tam giác ) hay BG < CG
Trong tam giác BDC: góc GBC đối diện với cạnh GC; góc GCB đối diện với cạnh GB mà GB < GC
=> góc GCB < GBC