Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a)
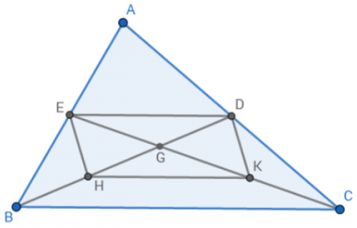
BD là đường trung tuyến của Δ ABC nên D là trung điểm của AC (1)
CE là đường trung tuyến của Δ ABC nên E là trung điểm của AB (2)
Từ (1) và (2) suy ra :
DE là đường trung bình của Δ ABC
=> DE // BC và DE = 1/2 BC
Δ BGC có H là trung điểm của GB và K là trung điểm của GC
suy ra HK là đường trung bình của Δ BGC
=> HK // BC và HK = 1/2 BC
Tứ giác DEHK có DE//BC, HK // BC và DE = HK = 1/2 BC
nên tứ giác
b) DEHK là hình bình hành nên
HG = GD = 1/2 HD và GE = GK = 1/2 EK
Để tứ giác DEHK là hình chữ nhật thì
HD = EK => 1/2 HD = 1/2 EK => GE = GD và GH = GK
GH = GK => 2GH = 2GK => GB = GC
Xét Δ GEB và Δ GDC có
GE = GD Góc EGB = góc DGC GB = GC => ΔGEB = ΔGDC (c.g.c) => BE = CD => 2BE = 2CD => AB = AC => ΔABC cân tại A Vậy đểtứ giác DEHK là hình chữ nhật thì
ΔABC cân tại Ac) BD ⊥ CE => HD ⊥ EK Hình bình hành DEHK có HD ⊥ EK nên DEHK là hình thoi Vậy
nếu các đường trung tuyến BD và CE vuông góc với nhau thì tứ giác DEHK là hình thoi

E là trung điểm của AB (CE là đường trung tuyến của tam giác ABC)
D là trung điểm của AC (BD là đường trung tuyến của tam giác ABC)
=> ED là đường trung bình của tam giác ABC.
=> ED // BC (1)
ED = BC/2 (2)
H là trung điểm của GB (gt)
K là trung điểm của GC (gt)
=> HK là đường trung bình của tam giác GBC.
=> HK // BC (3)
HK = BC/2 (4)
Từ (1) và (3)
=> ED // HK (5)
Từ (2) và (4)
=> ED = HK (6)
Từ (5) và (6)
=> DEHK là hình bình hành.
=> G là trung điểm của EK và HD.
=> EG = GK = EK/2
HG = GD = HD/2
CE là đường trung tuyến của tam giác ABC.
=> EG = CE/3
BD là đường trung tuyến của tam giác ABC.
=> DG = BD/3
DEHK là hình chữ nhật
<=> EK = HD
<=> EK/2 = HD/2
<=> EG = DG
<=> CE/3 = BD/3
<=> CE = BD
<=> Tam giác ABC cân tại A
Vậy DEHK là hình chữ nhật khi tam giác ABC cân tại A.
Hình bình hành DEHK có EK _I_ HD
=> DEHK là hình thoi.

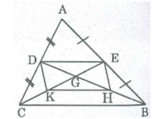
Hình bình hành DEHK trở thành hình chữ nhật khi DH = EK
Mà DH = 2/3 BD; EK = 2/3 CE
Nên DH = EK ⇒ BD = CE
⇒ ∆ ABC cân tại A.
Vậy ∆ ABC cân tại A thì tứ giác DEHK là hình chữ nhật.

Vì E,H là trung điểm AB,GB nên EH là đtb tg ABG
Do đó EH//AG và \(EH=\dfrac{1}{2}AG\)
Vì F,K là trung điểm CA,CG nên FK là đtb tg AGC
Do đó FK//AG và \(FK=\dfrac{1}{2}AG\)
\(\Rightarrow FK//EH\text{ và }FK=EH\\ \Rightarrow DEHK\text{ là hình bình hành}\)
Để DEHK là hv
\(\Leftrightarrow\left\{{}\begin{matrix}EH\perp HK\\EK\perp HD\end{matrix}\right.\left(1\right)\)
Ta có HK là đtb tg BGC nên HK//BC
Kết hợp \(\left(1\right)\Leftrightarrow\left\{{}\begin{matrix}AG\perp BC\left(EH//AG\right)\\BD\perp CE\end{matrix}\right.\)
Mà AG là trung tuyến nên ABC cân tại A
Vậy tam giác ABC cân tại A có trung tuyến BD,CE vuông góc với nhau thì DEHK là hình vuông




Nếu BD ⊥ CE ⇒ DH ⊥ EK
Hình bình hành DEHK có hai đường chéo vuông góc nên nó là hình thoi.