Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ta có:
\(M=\frac{2014-x}{x-2013}=\frac{2013-x+1}{x-2013}=\frac{2013-x}{x-2013}+\frac{1}{x-2013}=\frac{-\left(x-2013\right)}{x-2013}+\frac{1}{x-2013}=-1+\frac{1}{x-2013}\)
Để M có GTNN thì \(\frac{1}{x-2013}\) phải có GTNN
=> \(\frac{1}{x-2013}\) phải là số âm lớn nhất
Mà 1 là số nguyên dương không đổi nên x - 2013 = - 1
=> x = 2012
Khi đó, ta có:
\(M=\frac{2014-2012}{2012-2013}=\frac{2}{-1}=-2\)
Vậy M đạt GTNN là - 2 <=> x = 2012

Giải:
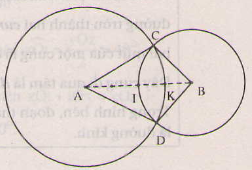
a) CA=2cm; DA= 3cm; CB= 2cm; DB= 2cm
b) Điểm I nằm giữa A và B nên
AI+ IB= AB= 4cm.
Mặt khác, IB= 2cm
Nên AI= 4 - 2 =2cm.
Vậy AI=IB(=2cm) suy ra I là trung điểm của AB.
c) Điểm I nằm giữa A và K nên
AI+ IK= AK,
Suy ra IK=AK-AI= 3-2 =1 cm.

Tổng đáy lớn và đáy bé là :
360.2 : 12 = 60 ( m )
Tổng số phần bằng nhau là :
2 + 3 = 5 ( phần )
Giá trị một phần là :
60 : 5 = 12 ( m )
Đáy bé là :
12.2 = 24 ( m )
Đáy lớn là :
12.3 = 36 ( m )
Đáp số : Đáy bé : 24 m
Đáy lớn : 36 m

Xét tứ giác FHDB có
\(\widehat{HFB}+\widehat{HDB}=180^0\)
Do đó: FHDB là tứ giác nội tiếp
Suy ra: \(\widehat{FDH}=\widehat{FBH}=\widehat{ABE}\left(1\right)\)
Xét tứ giác EHDC có
\(\widehat{HEC}+\widehat{HDC}=180^0\)
Do đó: EHDC là tứ giác nội tiếp
Suy ra: \(\widehat{EDH}=\widehat{ECH}=\widehat{ACF}\left(2\right)\)
Ta có: \(\widehat{ABE}+\widehat{BAC}=90^0\)
\(\widehat{ACF}+\widehat{BAC}=90^0\)
Do đó: \(\widehat{ABE}=\widehat{ACF}\left(3\right)\)
Từ (1), (2) và (3) suy ra \(\widehat{FDA}=\widehat{EDA}\)
hay DA là tia phân giác của góc FDE

tự vẽ hình nha:
+)Tam giác ABC có :D,E là trung điểm của AB và AC
\(\Rightarrow\)DE là đường trung bình của tam giác \(\Rightarrow\) DE//BC và DE=BC/2 (1)
+)Tam giác GBC có :I,K là trung điểm của GB,GC
\(\Rightarrow\)IK là đường trung bình của tam giác
\(\Rightarrow\)IK//BC và IK=BC/2 (2)
Từ (1) ,(2) \(\Rightarrow\)IK//DE và IK=DE
duong trung binh la gi?????////