Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
a) Gọi O là trung điểm của BC.
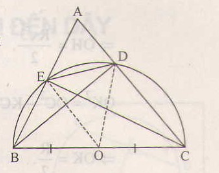
Theo tính chất trung tuyến ứng với cạnh huyền ta có:
EO=12BC;DO=12BC.EO=12BC;DO=12BC.
Suy ra OE=OD=OB=OC(=12BC)OE=OD=OB=OC(=12BC)
Do đó 4 điểm B, C, D, E cùng thuộc đường tròn (O) đường kính BC.
b) Xét đường tròn nói ở câu a), BC là đường kính, DE là một dây không qua tâm, do đó DE<BC.
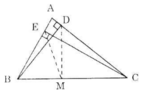
a) Gọi M là trung điểm của BC.
=> ME = MB = MC = MD
Do đó bốn điểm B, E, D, C cùng thuộc đường tròn tâm M. (đpcm)
b) Trong đường tròn tâm M nói trên, ta có DE là dây, BC là đường kính nên DE < BC.
Lời giải chi tiết
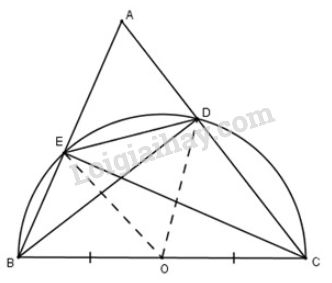
a) Gọi OO là trung điểm của BC⇒OB=OC=BC2.BC⇒OB=OC=BC2. (1)
Vì DODO là đường trung tuyến của tam giác vuông DBCDBC.
Theo tính chất trung tuyến ứng với cạnh huyền, ta có:
OD=12BCOD=12BC (2)
Từ (1) và (2) suy ra OD=OB=OC=12BCOD=OB=OC=12BC
Do đó ba điểm B, D, CB, D, C cùng thuộc đường tròn tâm OO bán kính OBOB.
Lập luận tương tự, tam giác BEC vuông tại E có EO là đường trung tuyến ứng với cạnh huyền BC nên OE=OB=OC=12BCOE=OB=OC=12BC
Suy ra ba điểm B, E, CB, E, C cùng thuộc đường tròn tâm OO bán kính OBOB.
Do đó 4 điểm B, C, D, EB, C, D, E cùng thuộc đường tròn (O)(O) đường kính BCBC.
b) Xét đường (O;BC2)(O;BC2), với BCBC là đường kính.
Ta có DEDE là một dây cung không đi qua tâm nên ta có BC>DEBC>DE ( vì trong một đường tròn, dây lớn nhất là đường kính).
a) Gọi \mathrm{M}M là trung điểm của \mathrm{BC}BC.
Ta có EM=\dfrac{1}{2} BC, DM=\dfrac{1}{2} BCEM=21BC,DM=21BC.
Suy ra ME=MB=MC=MDME=MB=MC=MD
do đó B, E, D, CB,E,D,C cùng thuộc đường tròn đường kính BCBC.
b) Trong đường tròn nói trên, DEDE là dây, BCBC là đường kính nên DE<BCDE<BC
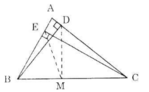
Gọi M là trung điểm của BC.
=> ME = MB = MC = MD
Do đó bốn điểm B, E, D, C cùng thuộc đường tròn tâm M. (đpcm)
A B C O E D
a) Gọi O là trung điểm của BC ( OB = OC )
+) Xét tam giác vuông EBC ( ^BEC = 90^o )
EO là đường trung tuyến
\(\Rightarrow EO=\frac{1}{2}BC\)
\(\Rightarrow OE=OB=OC\left(1\right)\)
+) Xét tam giác vuông DBC ( ^CDB = 90^o )
DO là đường trung tuyến \(\Rightarrow DO=\frac{1}{2}BC\)
=> DO = OB = OC (2)
Từ (1)(2) => OD = OE = OB = OC
Vậy : 4 điểm B , E , D , C cùng thuộc đường tròn đường trình BC ( đpcm )
a, B,C,D,E cùng thuộc đường tròn đường kính BC
b, BC là đường kính, ED dây không qua tâm => ĐPCM
a: Xét tứ giác AHCE có \(\hat{AHC}+\hat{AEC}=90^0+90^0=180^0\)
nên AHCE là tứ giác nội tiếp
=>A,H,C,E cùng thuộc một đường tròn
b: Sửa đề: Chứng minh BH=BD; DE là tiếp tuyến của đường tròn đường kính BC
Vì BC⊥AH tại H
nên BC là tiếp tuyến tại H của (A;AH)
Xét ΔAHB vuông tại H và ΔADB vuông tại D có
AB chung
AH=AD
Do đó: ΔAHB=ΔADB
=>BH=BD
Xét (O) có
BH,BD là các tiếp tuyến
Do đó: AB là phân giác của góc HAD
=>\(\hat{HAD}=2\cdot\hat{HAB}\)
Xét (O) có
CE,CH là các tiếp tuyến
Do đó: AC là phân giác của góc HAE
=>\(\hat{HAE}=2\cdot\hat{HAC}\)
\(\hat{DAE}=\hat{DAH}+\hat{EAH}\)
\(=2\cdot\left(\hat{HAB}+\hat{HAC}\right)=2\cdot\hat{BAC}=90^0\)
=>D,A,E thẳng hàng
mà AD=AE
nên A là trung điểm của DE
Gọi M là trung điểm của BC
=>M là tâm đường tròn đường kính BC
ΔABC vuông tại A
=>A nằm trên đường tròn đường kính BC
=>A nằm trên (M)
Ta có: BD⊥DE
CE⊥DE
Do đó: BD//CE
Xét hình thang BDEC có
M,A lần lượt là trung điểm của BC,DE
=>AM là đường trung bình của hình thang BDEC
=>AM//CE//BD
=>AM⊥DE tại A
=>ED là tiếp tuyến tại A của (M)
c:
Gọi X là giao điểm của EH và BD
Xét (A) có
ΔDHE nội tiếp
DE là đường kính
Do đó: ΔDHE vuông tại H
=>DH⊥EH tại H
=>DH⊥XE tại H
=>ΔDHX vuông tại H
Ta có: \(\hat{BHD}+\hat{BHX}=\hat{XHD}=90^0\)
\(\hat{BDH}+\hat{BXH}=90^0\) (ΔDHX vuông tại H)
mà \(\hat{BHD}=\hat{BDH}\)
nên \(\hat{BHX}=\hat{BXH}\)
=>BH=BX
mà BH=BD
nên BX=BD(1)
Ta có: HK⊥DE
XD⊥ED
Do đó: HK//XD
Xét ΔEDB có KI//DB
nên \(\frac{KI}{DB}=\frac{EI}{EB}\) (2)
Xét ΔEBX có IH//BX
nên \(\frac{IH}{BX}=\frac{EI}{EB}\) (3)
Từ (1),(2),(3) suy ra KI=HI
=>I là trung điểm của HK
a: Xét tứ giác BEDC có
\(\widehat{BEC}=\widehat{BDC}=90^0\)
Do đó: BEDC là tứ giác nội tiếp