Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Xet ΔCHA vuông tại H và ΔCKB vuông tại K có
góc C chung
=>ΔCHA đồng dạng với ΔCKB
b: Xét ΔCAB có
AH,BK là đừog cao
AH cắt BK tại D
=>D là trực tâm
=>CD vuông góc AB tại E
góc CHA=góc CEA=90 độ
=>CHEA nội tiếp
=>góc BHE=góc BAC
mà góc HBE chung
nên ΔBEH đồng dạng với ΔBAC
c: góc KHD=góc ACE
góc EHA=góc KBA
mà góc ACE=góc KBA
nên góc KHD=góc EHD
=>HA là phân giác của góc EHK

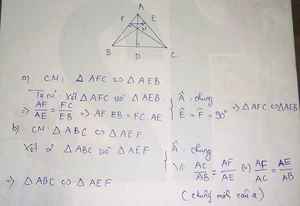
a: Xét ΔABE vuông tại E và ΔACF vuông tại F có
góc A chung
=>ΔABE đồng dạng với ΔACF
=>AB/AC=AE/AF
=>AB*AF=AE*AC: AB/AE=AC/AF
b: Xet ΔABC và ΔAEF có
AB/AE=AC/AF
góc BAC chung
=>ΔABC đồng dạng với ΔAEF
góc BFC=góc BDA=90 độ
mà góc B chung
nên ΔBFC đồng dạng với ΔBDA
=>BF/BD=BC/BA
=>BF/BC=BD/BA
=>ΔBFD đồng dạng với ΔBCA

a: Xet ΔIHB vuông tại H và ΔIKA vuông tại K có
góc HIB=góc KIA
=>ΔIHB đồng dạng với ΔIKA
=>IH/IK=IB/IA
=>IH*IA=IK*IB
b: Xet ΔBIA và ΔHIK có
IB/IH=IA/IK
góc BIA=góc HIK
=>ΔBIA đồng dạng với ΔHIK
c: AD là phân giác
=>BD/AB=CD/AC
=>BD/2=CD/3
=>3BD-2CD=0
mà BD-CD=-6
nên BD=12cm; CD=18cm

a: Xét ΔAEB vuông tại E và ΔAFC vuông tại F có
\(\widehat{BAE}\) chung
Do đó: ΔAEB\(\sim\)ΔAFC
b: Ta có: ΔAEB\(\sim\)ΔAFC
nên AE/AF=AB/AC
hay AE/AB=AF/AC
Xét ΔAEF và ΔABC có
AE/AB=AF/AC
\(\widehat{EAF}\) chung
DO đó: ΔAEF\(\sim\)ΔABC

a: Xét ΔAHC vuông tại H và ΔBKC vuông tại K có
góc C chung
Do đó: ΔAHC\(\sim\)ΔBKC
b: Ta có: ΔAHC\(\sim\)ΔBKC
nên HC/CK=AC/BC
=>6/CK=10/12=5/6
=>CK=7.2(cm)
a, Xét Δ AHC và Δ BKC, có :
\(\widehat{AHC}=\widehat{BKC}=90^o\)
\(\widehat{ACH}=\widehat{BCK}\) (góc chung)
=> Δ AHC ∾ Δ BKC (g.g)
b,
Ta có : AB = AC (Δ ABC cân tại A)
Mà AB = 10 (cm)
=> AC = 10 (cm)
Ta có :
Δ ABC cân tại A
AH là đường cao
=> AH là đường trung trực
=> 2HC = BC
=> 2HC = 12
=> HC = 6 (cm)
Ta có : Δ AHC ∾ Δ BKC (cmt)
=> \(\dfrac{AC}{BC}=\dfrac{HC}{KC}\)
=> \(\dfrac{10}{12}=\dfrac{6}{KC}\)
=> \(KC=\dfrac{12.6}{10}=7,2\left(cm\right)\)
Xét Δ BKC vuông tại C, có :
\(S_{\Delta_{BCK}}=\dfrac{1}{2}.CK.BC\)
=> \(S_{\Delta_{BCK}}=43,2\left(cm^2\right)\)

a) Xét ΔABC vuông tại A và ΔHBA vuông tại H có
\(\widehat{ABH}\) chung
Do đó: ΔABC\(\sim\)ΔHBA(g-g)
b) Xét ΔABC vuông tại A và ΔHBA vuông tại H có
\(\widehat{ABH}\) chung
Do đó: ΔABC\(\sim\)ΔHBA(g-g)