Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

1.

Xét tam giác vuông AHE có FI là đường trung tuyến ứng với cạnh huyền nên IF = IH = IA = AH/2 = 6 : 2 = 3 (cm)
Do IF = IH nên tam giác IHF cân tại I. Vậy thì \(\widehat{IFH}=\widehat{IHF}\)
Lại có \(\widehat{IHF}=\widehat{BHE}\) nên \(\widehat{IFH}=\widehat{BHE}\) (1)
Xét tam giác vuông BFC có FK là đường cao đồng thời là trung tuyến nên KF = KC = KB = BC : 2 = 4 (cm)
Ta cũng có KF = KB nên \(\widehat{HFK}=\widehat{HBK}\) (2)
Ta có \(\widehat{HBE}+\widehat{BHE}=90^o\) (3)
Từ (1), (2), (3) suy ra \(\widehat{IFH}+\widehat{HFK}=90^o\Rightarrow\widehat{IFK}=90^o\)
Xét tam giác vuông IFK, áp dụng định lý Pi-ta-go ta có:
IK2 = IF2 + FK2 = 32 + 42 = 25
\(\Rightarrow IK=5cm.\)
2.
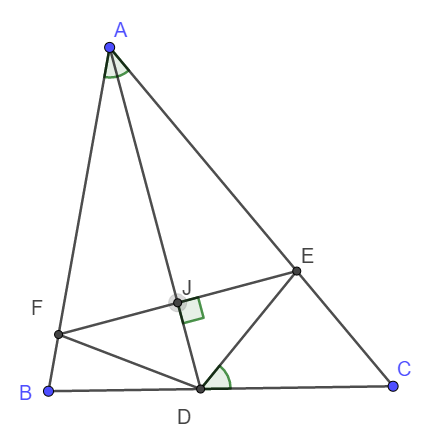
Gọi J là giao điểm của AD và EF.
Xét tam giác AFE có AJ là phân giác đồng thời đường cao nên AFE là tam giác cân tại A.
Vậy nên AJ đồng thời là trung trực của EF.
Lại có D thuộc AJ nên DE = DF. (1)
Xét tam giác AFD và tam giác AED có:
AF = AE
Cạnh AD chung
DF = DE
\(\Rightarrow\Delta AFD=\Delta AED\left(c-c-c\right)\)
\(\Rightarrow\widehat{AFD}=\widehat{AED}\Rightarrow\widehat{BFD}=\widehat{DEC}\)
Lại có \(\widehat{FBD}=180^o-\widehat{BAC}-\widehat{BCA}\)
\(\widehat{DEC}=180^o-\widehat{EDC}-\widehat{CBA}=180^o-\widehat{BAC}-\widehat{BCA}\)
Vậy nên \(\widehat{DBF}=\widehat{DFB}\) hay tam giác DBF cân tại D.
Suy ra DF = DB. (2)
Từ (1) và (2) suy ra DB = DF = DE.

BH=CK=căn 10^2-6^2=8cm
DF//KC
=>DF/KC= BD/BC
=>DF=BD/BC*8
DE//BH
=>DE/BH=CD/CB
=>DE=CD/CB*8
=>DF+DE=8

XÉT TAM GIÁC AHB VÀ TAM GIÁC AHC CÓ
AB=AC(GT)
AH CHUNG
GÓC AHB = GÓC AHC
=>TAM GIÁC AHB=TAM GIÁC AHC (CGC)
C,XÉT TAM GIÁC AHE VÀ TAM GIÁC AFH CÓ
AH CHUNG
GÓC AEH=GÓC AFH =90*
A1=A2
=>TAM GIÁC AHE=TAM GIÁC AFH (GCG)
=>HE=HF (CẠNH TƯƠNG ỨNG) A B C H
Xét tam giác ABH có:
AB^2 = BC.BH
hay 6^2 = 10.BH
suy ra: BH=3,6 (cm)
Tương tự: xét tam giác AHC có:
AC^2 = BC.HC
hay 8^2 = 10.HC
suy ra: HC=6,4 (cm)
Trong tam giác AHC có:
AC^2 = AH^2 + HC^2
hay 10^2 = AH^2 + 6,4^2
suy ra: AH= 7,7 (cm)
MÌNH BIẾT ĐƯƠC CÓ NHIÊU ĐÂY À, CHỪNG NÀO NGHĨ RA THÌ MÌNH LÀM THÊM NHA..!!!