
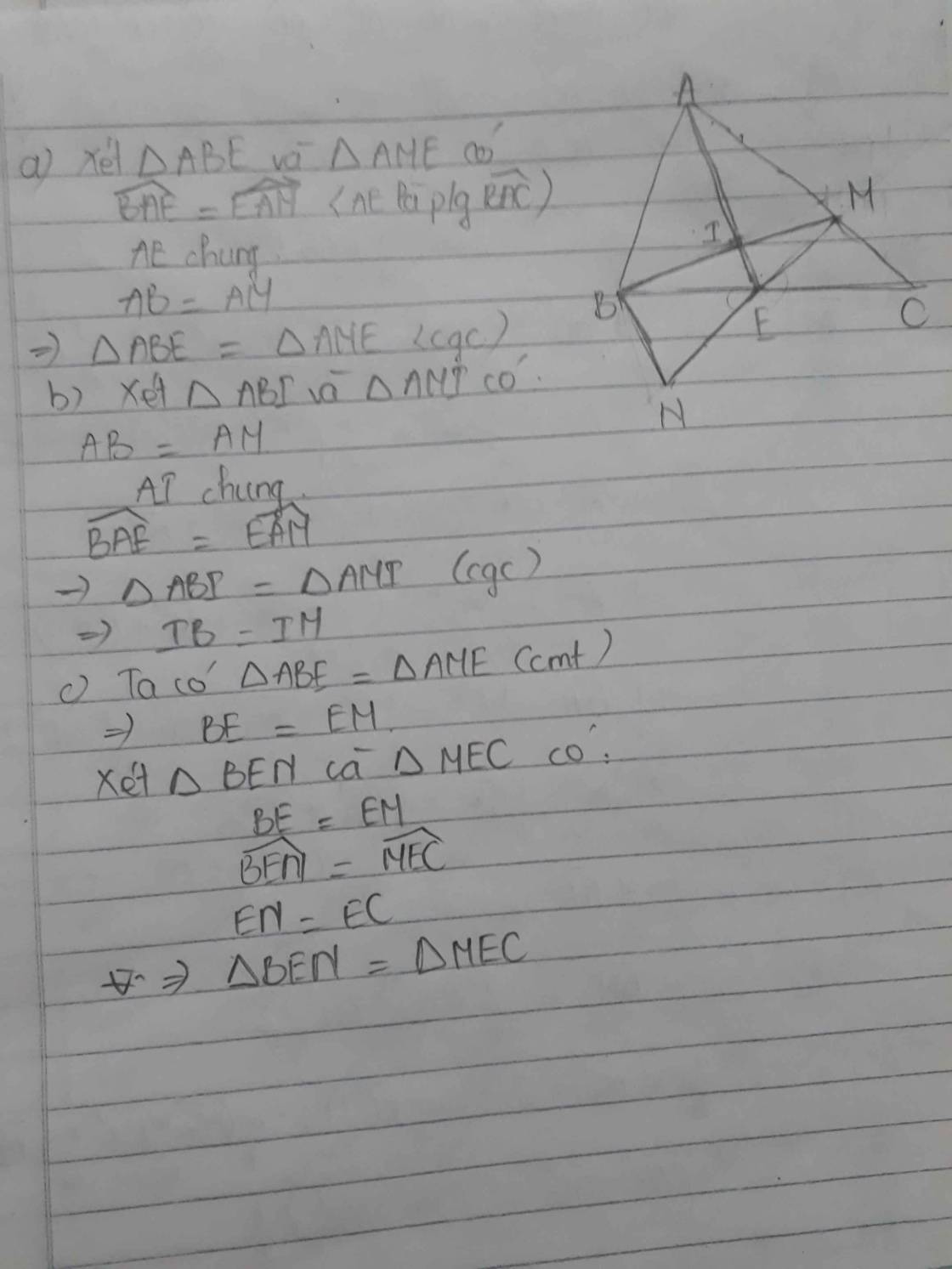
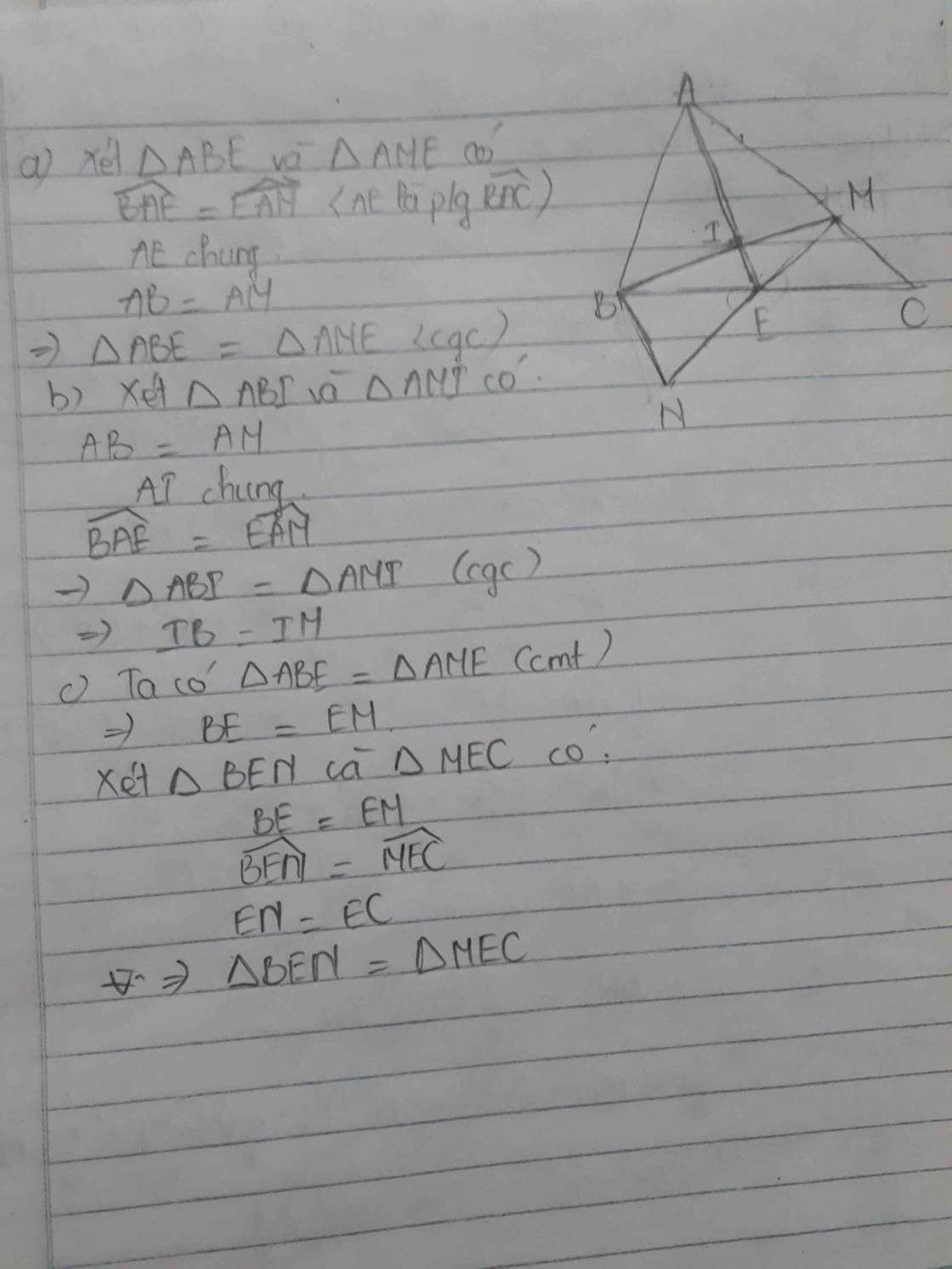 hình vẽ hơi xấu thông cảm :)))
hình vẽ hơi xấu thông cảm :)))
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

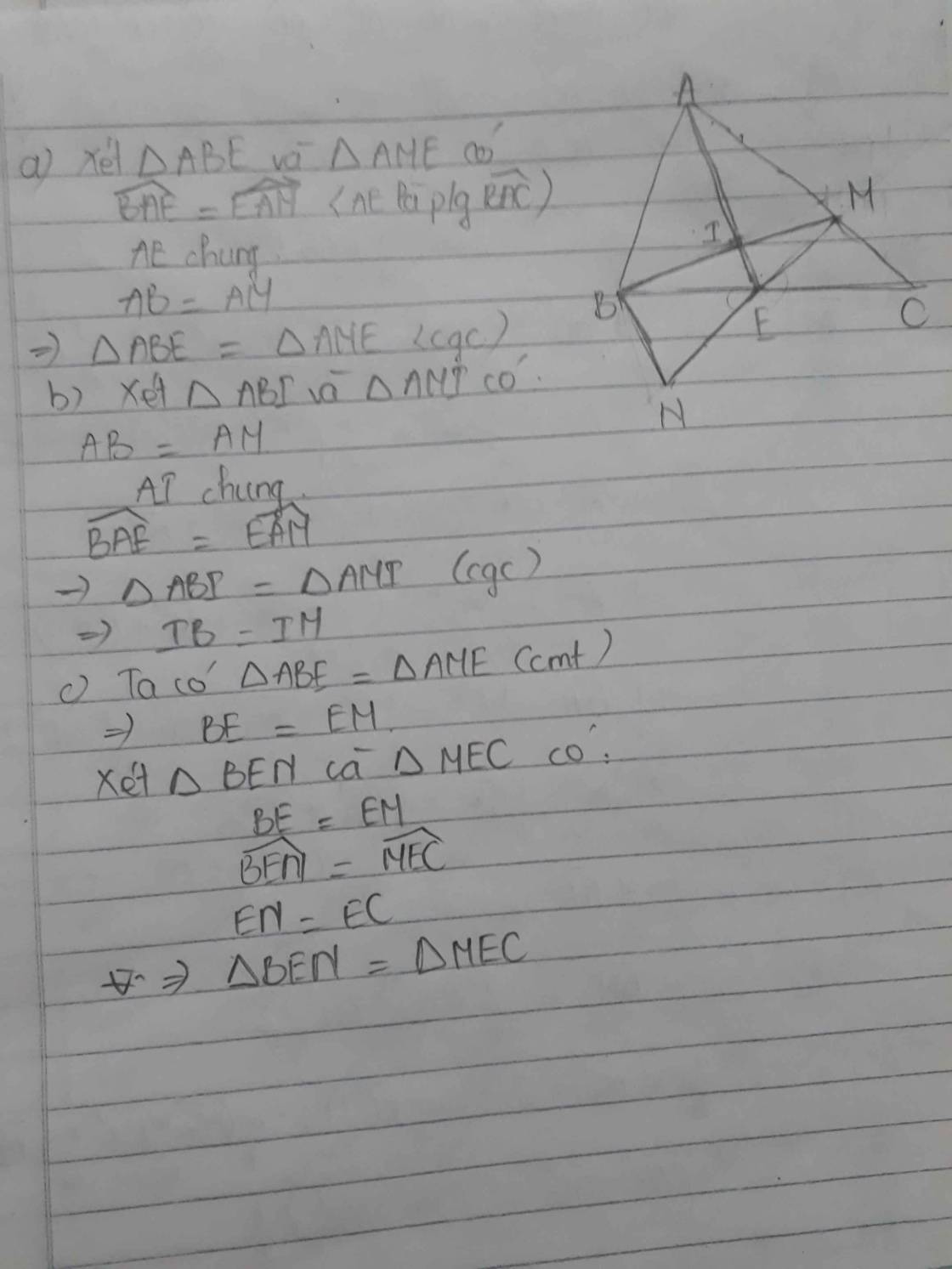
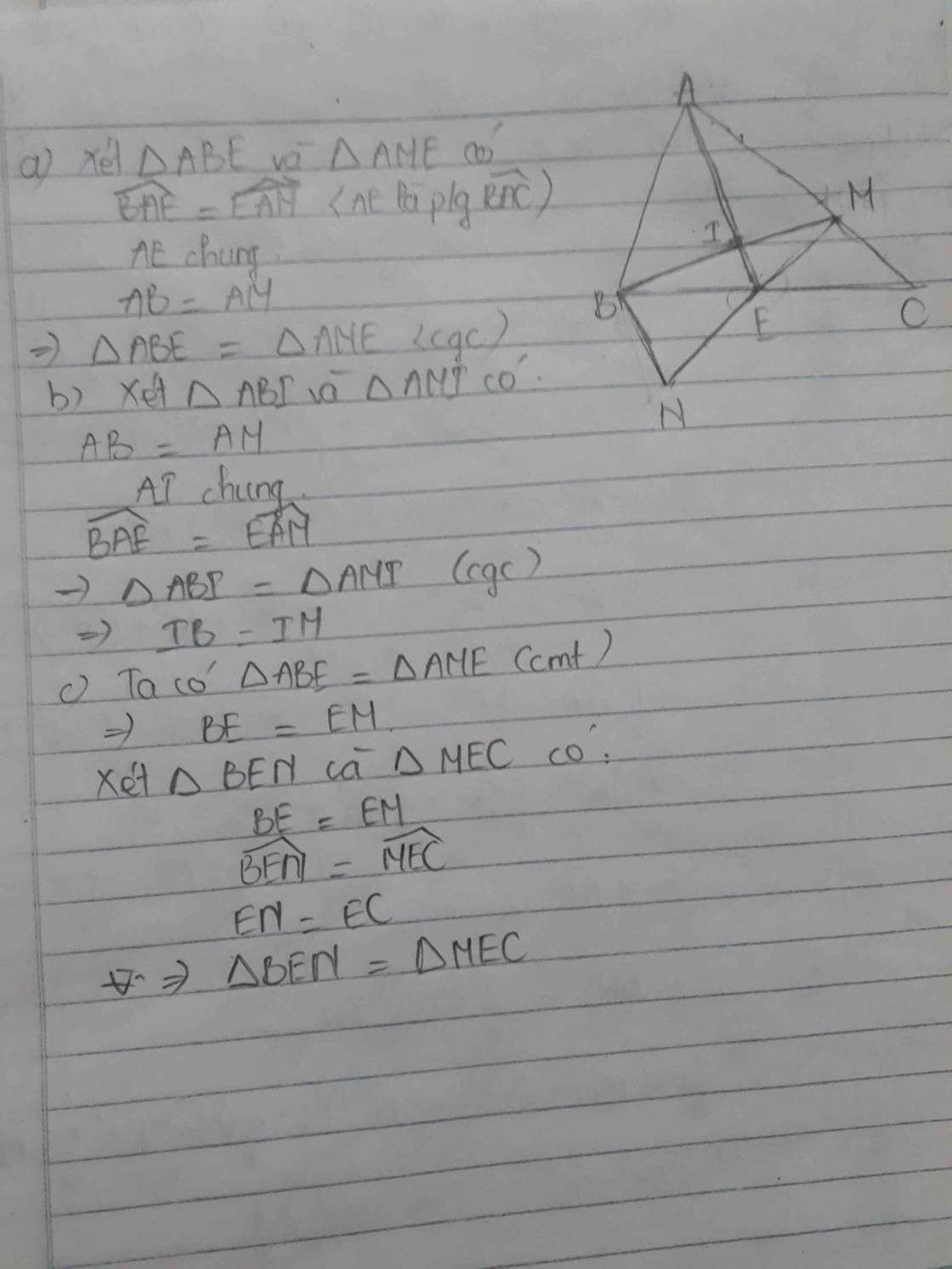 hình vẽ hơi xấu thông cảm :)))
hình vẽ hơi xấu thông cảm :)))

Sửa đề: Trên tia đối của tia EM lấy N sao cho EN=EC
a: Xét ΔABE và ΔAME có
AB=AM
\(\widehat{BAE}=\widehat{MAE}\)
AE chung
Do đó: ΔABE=ΔAME
b: Ta có: ΔABE=ΔAME
=>EB=EM
=>E nằm trên đường trung trực của BM(1)
Ta có: AB=AM
=>A nằm trên đường trung trực của BM(2)
Từ (1) và (2) suy ra AE là đường trung trực của BM
=>AE\(\perp\)BM tại I và I là trung điểm của BM
=>IB=IM
c: Xét ΔENB và ΔECM có
EN=EC
\(\widehat{NEB}=\widehat{CEM}\)(hai góc đối đỉnh)
EB=EM
Do đó: ΔENB=ΔECM
d: Ta có: ΔENB=ΔECM
=>\(\widehat{EBN}=\widehat{EMC}\)
mà \(\widehat{EMC}+\widehat{AME}=180^0\)(hai góc kề bù)
và \(\widehat{AME}=\widehat{ABE}\)(ΔAME=ΔABE)
nên \(\widehat{ABE}+\widehat{NBE}=180^0\)
=>A,B,N thẳng hàng

Khi đi học thêm và không có gì làm nên rảnh viết lại cái đề :))


a: Xét ΔBAD và ΔBMD có
BA=BM
góc ABD=góc MBD
BD chung
=>ΔBAD=ΔBMD
b: DA=DM
=>góc DAM=góc DMA

A)Xét tam giác ABD và EBD
DB chung
\(\widehat{EBD}=\widehat{DBA}\)
AB=AE
=> tam giác ABD = tam giác EBD
B)DE=AD
DE\(⊥\)BC
Xét tam giác vuông DEC và DAM
\(\widehat{CDE}=\widehat{MDA}\)
AD=DE
=> tam giác ADM = tam giác EDC => CE =AM
C) MÌNH KO BIẾT