Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

A B C I J R S P Q
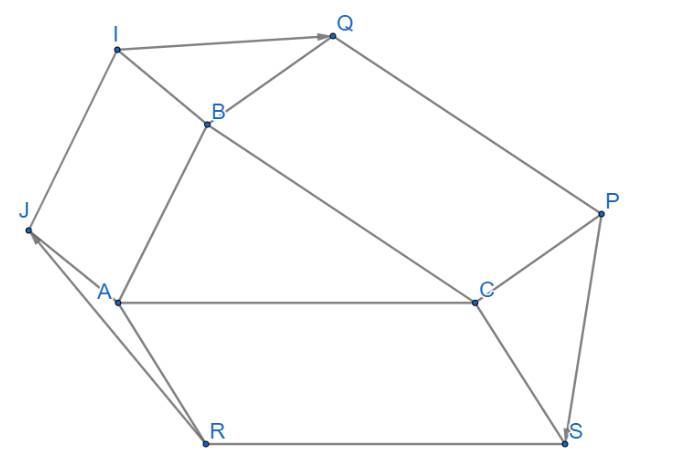
Có \(\overrightarrow{RJ}+\overrightarrow{IQ}+\overrightarrow{PS}=\overrightarrow{RA}+\overrightarrow{AJ}+\overrightarrow{IB}+\overrightarrow{BQ}+\overrightarrow{PC}+\overrightarrow{CS}\)
\(=\left(\overrightarrow{RA}+\overrightarrow{CS}\right)+\left(\overrightarrow{AJ}+\overrightarrow{IB}\right)+\left(\overrightarrow{BQ}+\overrightarrow{PC}\right)\)
\(=\overrightarrow{0}+\overrightarrow{0}+\overrightarrow{0}=\overrightarrow{0}\). ( Do tứ giác ABIJ, BCPQ, CARS là hình bình hành).
Vậy \(\overrightarrow{RJ}+\overrightarrow{IQ}+\overrightarrow{PS}=\overrightarrow{0}\).

\(\overrightarrow {RJ} + \overrightarrow {IQ} + \overrightarrow {PS} = \left( {\overrightarrow {RA} + \overrightarrow {AJ} } \right) + \left( {\overrightarrow {IB} + \overrightarrow {BQ} } \right) + \left( {\overrightarrow {PC} + \overrightarrow {CS} } \right)\)
\( = \left( {\overrightarrow {RA} + \overrightarrow {CS} } \right) + \left( {\overrightarrow {AJ} + \overrightarrow {IB} } \right) + \left( {\overrightarrow {BQ} + \overrightarrow {PC} } \right) = \overrightarrow 0 + \overrightarrow 0 + \overrightarrow 0 = \overrightarrow 0 \)\(\)(đpcm)

bài 1) ta có \(\overrightarrow{AQ}=\overrightarrow{AM}+\overrightarrow{MN}+\overrightarrow{NP}+\overrightarrow{PQ}=\overrightarrow{BA}+\overrightarrow{DA}+\overrightarrow{DC}+\overrightarrow{BC}\)
\(=\left(\overrightarrow{BA}+\overrightarrow{BC}\right)+\left(\overrightarrow{DA}+\overrightarrow{DC}\right)=\overrightarrow{BD}+\overrightarrow{DB}=\overrightarrow{0}\left(đpcm\right)\)
bài 2) bn tham khảo nha : https://hoc24.vn/hoi-dap/question/636668.html

Bạn xem lại đề ạ!
Nếu bạn đã chứng minh được D là trung điểm IQ; E là trung điểm KP; E là trung điểm KP; F là trung điểm LJ
Thì dễ dàng suy ra được: \(\overrightarrow{MD}=\frac{\overrightarrow{MI}+\overrightarrow{MQ}}{2}\); \(\overrightarrow{ME}=\frac{\overrightarrow{MK}+\overrightarrow{MP}}{2}\); \(\overrightarrow{MF}=\frac{\overrightarrow{MJ}+\overrightarrow{ML}}{2}\)
( Vì chúng ta có tính chất: Nếu I là trung điểm đoạn thẳng AB thì mọi điểm M ta có: \(2\overrightarrow{MI}=\overrightarrow{MA}+\overrightarrow{MB}\))

Ta đã biết nếu G' là trọng tâm tam giác ABC thì:
\(\overrightarrow{G'A}+\overrightarrow{G'B}+\overrightarrow{G'C}=\overrightarrow{0}\).
Gỉa sử có điểm G thỏa mãn: \(\overrightarrow{GA}+\overrightarrow{GB}+\overrightarrow{GC}=\overrightarrow{0}\).
Ta sẽ chứng minh \(G\equiv G'\).
Thật vậy:
\(\overrightarrow{GA}+\overrightarrow{GB}+\overrightarrow{GC}=\overrightarrow{0}\)
\(\Leftrightarrow3\overrightarrow{GG'}+\overrightarrow{G'A}+\overrightarrow{G'B}+\overrightarrow{G'C}=\overrightarrow{0}\)
\(\Leftrightarrow3\overrightarrow{GG'}=\overrightarrow{0}\)
\(\Leftrightarrow\overrightarrow{GG'}=\overrightarrow{0}\).
Vậy \(G\equiv G'\).
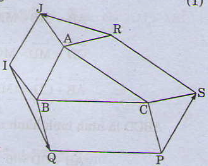
\(\overrightarrow{RF}+\overrightarrow{IQ}+\overrightarrow{PS}=\overrightarrow{RA}+\overrightarrow{AF}+\overrightarrow{IB}+\overrightarrow{BQ}+\overrightarrow{PC}+\overrightarrow{CS}=\overrightarrow{0}\)
ta có : \(\overrightarrow{RF}+\overrightarrow{IQ}+\overrightarrow{PS}\)
\(=\overrightarrow{RA}+\overrightarrow{AB}+\overrightarrow{BF}+\overrightarrow{IB}+\overrightarrow{BC}+\overrightarrow{CQ}+\overrightarrow{PC}+\overrightarrow{CA}+\overrightarrow{AS}\)
\(=\overrightarrow{RA}+\overrightarrow{BF}+\overrightarrow{IB}+\overrightarrow{CQ}+\overrightarrow{PC}+\overrightarrow{AS}\) \(=\overrightarrow{RS}+\overrightarrow{IF}+\overrightarrow{PQ}=\overrightarrow{AC}+\overrightarrow{BA}+\overrightarrow{CB}=\overrightarrow{0}\left(đpcm\right)\)