Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

c.
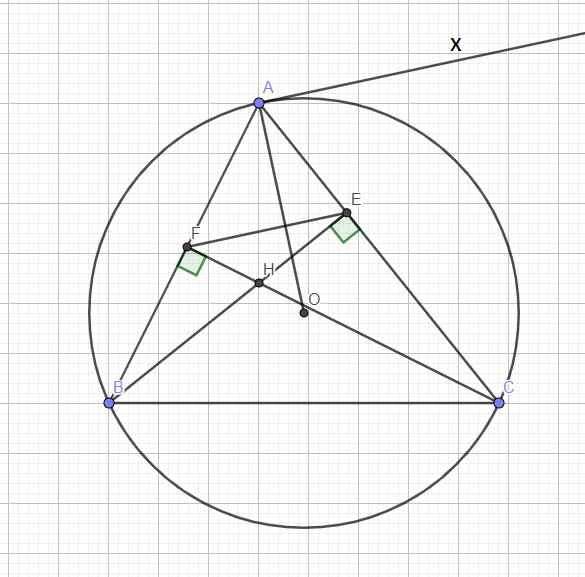
Qua A kẻ tiếp tuyến \(Ax\Rightarrow Ax\perp OA\) (1)
Do E và F cùng nhìn BC dưới 1 góc vuông
\(\Rightarrow\) Tứ giác BCEF nội tiếp
\(\Rightarrow\widehat{CEF}+\widehat{CBF}=180^0\)
Mà \(\widehat{CEF}+\widehat{AEF}=180^0\)
\(\Rightarrow\widehat{CBF}=\widehat{AEF}\)
Lại có \(\widehat{CBF}=\widehat{CAx}\) (cùng chắn AC)
\(\Rightarrow\widehat{AEF}=\widehat{CAx}\)
\(\Rightarrow Ax||EF\) (hai góc so le trọng bằng nhau) (2)
\(\left(1\right);\left(2\right)\Rightarrow OA\perp EF\)

Bạn tự vẽ hình nha ^-^
a, Xét tứ giác BFEC có:
BFC=BEC =90 mà 2 góc này cùng nhìn cạnh BC
nên tứ giác BFEC nội tiếp
b,Ta thấy
BPQ= 1/2 cung BQ
BCQ=1/2 cung BQ
nên BPQ=BCQ
c,Tứ giác BFEC nội tiếp nên EBC=EFC (cùng nhìn cạnh EC)
và PBC=PQC (góc nội tiếp cùng chắn cung PC)
nên CFE=CQP (=PBC)
mà 2 góc ở vị trí đồng vị nên EF//QP
d, Kéo dài OA cắt đường tròn (O,R) tại I
ta có :AEF=ABC=1/2 cung AC
IAC =1/2 cung IC
nên AEF+IAC=1/2(cung AC+cung IC)=1/2 cung AI=90
vậy AO vuông góc với EF
a, Xét tứ giác BFEC có:
BFC=BEC =90 mà 2 góc này cùng nhìn cạnh BC
nên tứ giác BFEC nội tiếp
b,Ta thấy
BPQ= 1/2 cung BQ
BCQ=1/2 cung BQ
nên BPQ=BCQ
c,Tứ giác BFEC nội tiếp nên EBC=EFC (cùng nhìn cạnh EC)
và PBC=PQC (góc nội tiếp cùng chắn cung PC)
nên CFE=CQP (=PBC)
mà 2 góc ở vị trí đồng vị nên EF//QP
d, Kéo dài OA cắt đường tròn (O,R) tại I
ta có :AEF=ABC=1/2 cung AC
IAC =1/2 cung IC
nên AEF+IAC=1/2(cung AC+cung IC)=1/2 cung AI=90
vậy AO vuông góc với EF

A) GÓC BFC=BIC CUNG NHÌN BC DƯỚI MOOTF GÓC=90 \(\Rightarrow\) BCEF NỘI TIẾP
B) VÌ BCEF NỒI TIẾPÓC MBC=CFE
GÓC MNC=MBC(=1/2SĐ CUNG MC)
\(\Rightarrow\) GÓC MNC=CFE\(\Rightarrow\) MN//È
C) VÌ BCEF NỘI TIẾP GÓC FBM=FCE
MÀ FBM=1/2 SĐ CUNG AN , FCE=1/2 SĐ CUNG AM \(\Rightarrow\)CUNG AN=CUNG AM ĐI QUA TRUNG ĐIỂM VUÔNG GÓC È
a: Xét tứ giác AEHF có \(\widehat{AEH}+\widehat{AFH}=90^0+90^0=180^0\)
nên AEHF là tứ giác nội tiếp
b: Xét ΔFAC vuông tại F và ΔFHB vuông tại F có
\(\widehat{FCA}=\widehat{FBH}\left(=90^0-\widehat{BAE}\right)\)
Do đó: ΔFAC đồng dạng với ΔFHB
=>\(\dfrac{FA}{FH}=\dfrac{FC}{FB}\)
=>\(FA\cdot FB=FC\cdot FH\)
c: Xét tứ giác BFEC có \(\widehat{BFC}=\widehat{BEC}=90^0\)
nên BFEC là tứ giác nội tiếp
=>\(\widehat{FEC}+\widehat{FBC}=180^0\)
mà \(\widehat{FEC}+\widehat{AEF}=180^0\)(hai góc kề bù)
nên \(\widehat{AEF}=\widehat{ABC}\)(1)
Kẻ tiếp tuyến Ax của (O)
Xét (O) có
\(\widehat{xAC}\) là góc tạo bởi tiếp tuyến Ax và dây cung AC
\(\widehat{ABC}\) là góc nội tiếp chắn cung AC
Do đó: \(\widehat{xAC}=\widehat{ABC}\left(2\right)\)
Từ (1),(2) suy ra \(\widehat{xAC}=\widehat{AEF}\)
mà hai góc này là hai góc ở vị trí so le trong
nên Ax//FE
Ta có: Ax//FE
OA\(\perp\)Ax
Do đó: OA\(\perp\)EF