Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Hình tự vẽ.
a) Ta có: AB=AC
\(\Rightarrow\Delta\)ABC cân
Xét \(\Delta\)AHB và \(\Delta\)AHC có:
AHB=AHC (=90o)
AH: chung
ABH=ACH (\(\Delta\)ABC cân)
\(\Rightarrow\)\(\Delta\)AHB=\(\Delta\)AHC (g.c.g)
\(\Rightarrow\)HAB=HAC (2 góc tương ứng)
\(\Rightarrow\)AH là phân giác BAC
b) Xét \(\Delta\)AHK và \(\Delta\)AHQ có:
AKH=AQH (=90o)
AH: chung
HAK=HAQ (cm câu a)
\(\Rightarrow\Delta\)AHK=\(\Delta\)HAQ (ch-gn)
Ta có:
AK+KB=AB
AQ+QC=AC
Mà AB=AC (gt)
AK=AQ (\(\Delta\)AHK=\(\Delta\)AHQ)
\(\Rightarrow\)KB=QC
Xét \(\Delta\)KBH và \(\Delta\)QCH có:
HK=HQ (\(\Delta\)AHK=\(\Delta\)AHQ)
HB=HC (\(\Delta\)AHB=\(\Delta\)AHC)
KB=QC (cmt)
\(\Rightarrow\Delta\)KBH=\(\Delta\)QCH (c.c.c)
\(\Rightarrow\)HK=HQ (2 cạnh tương ứng)
c) Xét \(\Delta\)KBM và \(\Delta\)QCN có:
KMB=QNC (=90o)
KB=QC (cmt)
KBM=QCN (\(\Delta\)ABC cân)
\(\Rightarrow\Delta\)KBM=\(\Delta\)QCN (ch-gn)
\(\Rightarrow\)KM=QN (2 cạnh tương ứng)
Mới làm đc 1 cách :))

Giải
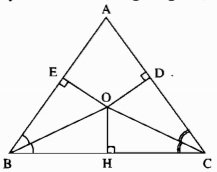
Kẻ OH⊥BC
Xét hai tam giác vuông OEB và OHB, ta có:
\(\widehat{\text{OEB}}=\widehat{\text{OHB}}\)=90o
Cạnh huyền OB chung
\(\widehat{EBO}=\widehat{\text{HB}O}\)(gt)
Suy ra: ∆OEB = ∆OHB (cạnh huyền, góc nhọn)
⇒ OE = OH (hai cạnh tương ứng) (1)
Xét hai tam giác vuông OHC và ODC, ta có:
\(\widehat{\text{OHC}}=\widehat{\text{ODC}}\)=90oCạnh huyền OC chung
\(\widehat{\text{HCO}}=\widehat{\text{DCO}}\)(gt)
Suy ra: ∆OHC = ∆ODC (cạnh huyền, góc nhọn)
⇒ OH = OD (hai cạnh tương ứng) (2)
Từ (1) và (2) suy ra: OE = OD.

a: Ta có: ˆABD=ˆBAMABD^=BAM^
ˆDBC=ˆAMBDBC^=AMB^
mà ˆABD=ˆDBCABD^=DBC^
nên ˆBAM=ˆAMB

a: Xét ΔABD vuông tại D và ΔACE vuông tại E có
AB=AC
\(\widehat{BAD}\) chung
Do đó: ΔABD=ΔACE
Suy ra:BD=CE
b: Xét ΔAEO vuông tại E và ΔADO vuông tại D có
AO chung
AE=AD
Do đó: ΔAEO=ΔADO
Suy ra: OE=OD
c: Ta có: OE+OC=EC
OD+OB=DB
mà EC=DB
và OE=OD
nên OC=OB
d: Xét ΔABO và ΔACO có
AB=AC
BO=CO
AO chung
Do đó: ΔABO=ΔACO
Suy ra: \(\widehat{BAO}=\widehat{CAO}\)
hay AO là tia phân giác của góc BAC

hình Imgur: Sự kỳ diệu của Internet : https://imgur.com/a/OpRrWs8
a) nhìn hình cũng đủ thấy \(\Delta ABC>\Delta ACH\)
hai tam giác không tương ứng
\(\Delta ACH=\frac{1}{2}\Delta ABC\)
thực chất mình cũng không biết cách cm nó k bằng nhau :3
b) Vì H là tia phân giác của \(\widehat{BAC}\)
\(\Rightarrow\Delta ABH=\Delta ACH\left(c.g.c\right)\)
\(\widehat{H_1}=\widehat{H_2}\)( 2 góc kề bù mà H là tia phân giác )
\(\Rightarrow\widehat{H_1}+\widehat{H_2}=180^o\)
\(\Rightarrow2H_1=\frac{180^o}{2}=90^o\)
\(\Rightarrow AH\perp BC\)(1)
c) gọi I là trung điểm của cạnh DE
cm giống như trên
\(\Rightarrow AI\perp DE\)(2)
Từ (1) và (2) ta có :
\(\Rightarrow\hept{\begin{cases}AH\perp BC\\AI\perp DE\end{cases}}\)
=> DE // BC
\(I\in AH\)nên vẫn có thể cm theo kiểu đó maybe ....
không chắc đâu:)
A B C O D E F a) Có \(8^2\) = 64 ; \(15^2\) = 225 ; \(17^2\) = 289
Vì 64+225 =289 => \(8^2+15^2=17^2\)
Áp dụng dịnh lý py-ta-go đảo vào \(\Delta\)ABC có
\(8^2+15^2=17^2\) => \(AB^2+AC^2=BC^2\)
=> \(\Delta\)ABC vuông tại A (đpcm)
b) Vì O là giao điểm của 2 đường phân giác trong \(\Delta ABC\)
=> O là điểm chung của 3 đường phân giác trong \(\Delta ABC\) (tính đồng quy trong tam giác)
Lại có \(OD\perp BC;OE\perp AB;OF\perp AC\)
=> OD;OE;OF là khoảng cách từ O tới 3 cạnh \(\Delta ABC\)
=>OD = OE = OF (tc 3 đường phân giác trong tam giác) (đpcm)
c) Theo chứng minh ở câu b có O là điểm chung của 3 đường phân giác trong \(\Delta ABC\)
=>O phải thuộc 3 đường phân giác trong \(\Delta ABC\)
=>OA là phân giác của góc BAC (đpcm)
d) mk chưa nghĩ ra