Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Bài 4:
Gọi M là giao điểm của EF với BC, N là giao điểm của DF với AB, ta có:
Ta có: DF vuông góc với AH
BC vuông góc với AH
DF song song với BC (hay BM) (2 góc trong cùng phía)
Mà là góc ngoài của nên
AB song song với MF (hay EF) (vì có 2 góc đồng vị bằng nhau) (1)
(2 góc so le trong)
Xét và có:
AH = DE (vì AD +DH = DH + HE)
(ch/minh trên)
(cạnh góc vuông - góc nhọn) DF = BH (2 cạnh tương ứng)
Xét và có:
HE = AD (gt)
BH = DF (ch/minh trên)
(2 cạnh góc vuông) (2 góc tương ứng)
BE song song với AF (hay AC) (vì có 2 góc so le trong bằng nhau) (2)
Mặt khác: BA vuông góc với AC (3)
Từ (1), (2) và (3) suy ra: BE vuông góc với EF (đpcm)

Hình tự vẽ
Xét \(\Delta MBH\)và \(\Delta NCH\)
\(\widehat{BMH}=\widehat{CNH}=90^o\)
\(BH=CH\left(cma\right)\)
\(\widehat{NBH}=\widehat{NQH}\)(Tam giác ABC cân tại A
\(\Rightarrow\Delta MBH=\Delta NCH\left(ch-gn\right)\)
\(MH=NH\left(2ctu\right)_{\left(1\right)}\)
Xét \(\Delta BQH\)và \(\Delta CNH\)
\(\widehat{Q}=\widehat{CNH}=90^o\)
\(BH=CH\left(cma\right)\)
\(\widehat{BHQ}=\widehat{NHC}\)(đối đỉnh)
\(\Rightarrow\Delta BQH=\Delta CNH\left(ch-gn\right)\)
\(\Rightarrow QH=NH\left(2ctu\right)_{\left(2\right)}\)
Từ \(\left(1\right),\left(2\right)\Rightarrow MH=QH\)
=> \(\Delta HQM\)cân tại H
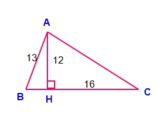
Cho tam giác nhọn ABC. Kẻ AH vuông góc với BC (H thuộc BC). Biết AB=13cm,AH=12cm,HC=16cm. Tính AC,BC

Xét tam giác AHC có góc AHC=90
=>Tam giác AHC vuông tai H
Áp dụng định lí Py ta go cho tam giác AHC , ta có
AH^2+HC^2=AC^2
=>12^2+16^2=AC^2
=>400=AC^2
=>AC=20(cm)
Áp dụng định lí Py ta go cho tam giác AHB , ta có
AH^2+HB^2=AB^2
=>12^2+HB^2=13^2
=>HB^2=25
=>HB=5(cm)
Ta có BH+HC=BC
=>5+16=BC
=>BC=21 (cm)
Vậy AC=20cm ; BC=21cm

Ta có : AC^2=AH^2+HC^2 (định lí Pytago trong tam giác vuông ACH)
AC^2=12^2+16^2 AC^2=144+256 AC^2=400 AC=Căn 400=20(cm)
Ta có : AB^2=AH^2+HB^2 (định lí Pytago trong tam giác vuông ABH) 13^2=12^2+HB^2 169=144+HB^2 HB^2=169-144 HB^2=25
HB=Căn 25=5(cm) Ta có : BC=HB+HC BC=5+16 BC=21(cm)
A B C H (Hình minh hoạ) AB = 13 cm, AH = 12 cm, HC = 16 cm
AH vuông góc với BC => Tam giác ABH và tam giác ACH vuông tại A
Áp dụng định lí Pi- ta - go trong tam giác AHC, có:
AC2 = AH2 + HC2
AC2 = 122 + 162 = 400 => AC = 20 cm
Áp dụng đinh lí Pi - ta -go trong tam giác ABH, có:
AB2 = AH2 + BH2
132 = 122 + BH2 => BH2 = 132 - 122 = 25 => BH = 5 cm
mà HC + BH = BC
16 + 5 = 21 = BC
Vậy AC = 20 cm, BC = 21 cm

a/ Xét tam giác ABH vuông tại H và tam giác AHC vuông tại H
. AB = AC ( tam giác ABC cân tại A )
. AH là cạnh chung
Suy ra tam giác ABH = tam giác AHC ( cạnh huyền - cạnh góc vuông )
Mà H thuộc BC
Suy ra H là trung điểm của BC
Suy ra BH = BC ( 2 cạnh tương ứng )
b/ Xét tam giác AHC vuông tại H có
AC2 = AH2 + HC2 ( định lý pytago )
132 = 122 + HC2
169= 144 + HC2
HC2 = 169 -144
HC2 = 25
HC =\(\sqrt{25}\)
HC = 5 cm
=> Bc =HC .2 =10cm
Vậy BC = 10cm
c/ Xét tam giác AEM vuông tại M và tam giác EMB vuông tại M
. EM là cạnh chung
.AM = MB ( M là trung điểm )
=> Tam giác AEM = tam giác EMB ( cạnh huyền - cạnh góc vuông )
=> A1 = B1 ( 2 góc ở đáy )
=> AE =BE ( 2 cạnh tương ứng )
=> Tam giác AEB cân tại E
d/ Ta có:
. A1 = A2 ( tam giác ABH = tam giác ACH )
. B1 = A2 ( tam giác ABE cân )
=> B1 = A1
Xét tam giác BDE và tam giác AFE có
. BD = AF ( gt )
. BE = AE ( tam giác ABE cân tại E )
.B1 = A1 ( cmt )
=> Tam giác DEB = tam giác AFE( c.g.c )
=> ED = EF ( 2 cạnh tương ứng )
Tam giác DEF có
DE + EF > DF ( bất đẳng thức tam giác)
Mà DE = EF ( cmt )
=> EF + EF > DF
=> 2EF > DF
=> EF > \(\frac{DF}{2}\)

Ta có : AC^2=AH^2+HC^2 (định lí Pytago trong tam giác vuông ACH) AC^2=12^2+16^2 AC^2=144+256 AC^2=400 AC=Căn 400=20(cm) Ta có : AB^2=AH^2+HB^2 (định lí Pytago trong tam giác vuông ABH) 13^2=12^2+HB^2 169=144+HB^2 HB^2=169-144 HB^2=25 HB=Căn 25=5(cm) Ta có : BC=HB+HC BC=5+16 BC=21(cm)
áp dụng pitago tính đc BH cộng đoạn thẳng tính đc BC,áp dụng pitago tính đc AC

AC^2=AH^2+HC^2(py ta go)
AC^2=144+256=200 cm
suy ra AC=20 cm
AB^2=AH^2+BH^2
BH^2=AB^2-AH^2
BH^2=1169-144=25cm
BH=5cm
Mà BH+HC=BC suy ra 5+16=21
vạy AC=20 cm, BC=21cm

Áp dụng định lí Pi-ta-go trong ΔAHC vuông tại H ta có:
AC2 = AH2 + HC2 = 122 + 162 = 144 + 256 = 400
⇒ AC = 20 (cm)
Áp dụng định lí Pi-ta-go trong ΔAHB vuông tại H ta có:
BH2 + AH2 = AB2 ⇒ BH2 = AB2 - AH2 = 132 - 122 = 169 -144 = 25
⇒ BH = 5cm
Do đó BC = BH + HC = 5 + 16 = 21 (cm)
Áp dụng định lí pitago vào tgiac ABH vuông tại H có:
BH^2=AB^2-AH^2=!3^2-12^2=25
=>BH=5(cm)
Áp dụng định lí pitago vào tam giác AHC vuông tại H có:
AC^2=AH^2+HC^2=12^2+16^2=400
=> AC=20(cm)
Ta có HM=AM=MC( vì trong một tam giác vuông đường trung tuyến ứng với cạnh huyền thì bằng nửa cạnh huyền)
=> HM=10(cm)
*** cho mk nha ^^!
Hình như thiếu cạnh BC bạn ạ