Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
cần cm IB=KM từ đó có AI=AK . suy ra tgAPK cân tại A. suy ra góc AKP=gocsIAD. từ đó có dpcm
| GT | △ABC : AB < AC. D BC ∩ AM = {K} |
| KL | DK = CK |
AB : AD = AC. DAM = MAC = BAC /2. M Cách 1:
Xét △DAM và △CAM
Có: AD = AC (gt)
DAM = CAM (gt)
AM là cạnh chung
=> △DAM = △CAM (c.g.c)
=> MD = CM (2 cạnh tương ứng)
và AMD = AMC (2 góc tương ứng)
Mà AMD + AMC = 180o (2 góc kề bù)
=> AMD = AMC = 180o/2 = 90o
Xét △DMK vuông tại M và △CMK vuông tại M
Có: KM là cạnh chung
DM = CM (cmt)
=> △DMK = △CMK (2 cgv)
=> DK = CK (2 cạnh tương ứng)
Cách 2:
Xét △DAK và △CAK
Có: AD = AC (gt)
DAK = CAK (gt)
AK là cạnh chung
=> DAK = CAK (c.g.c)
=> DK = CK (2 cạnh tương ứng)
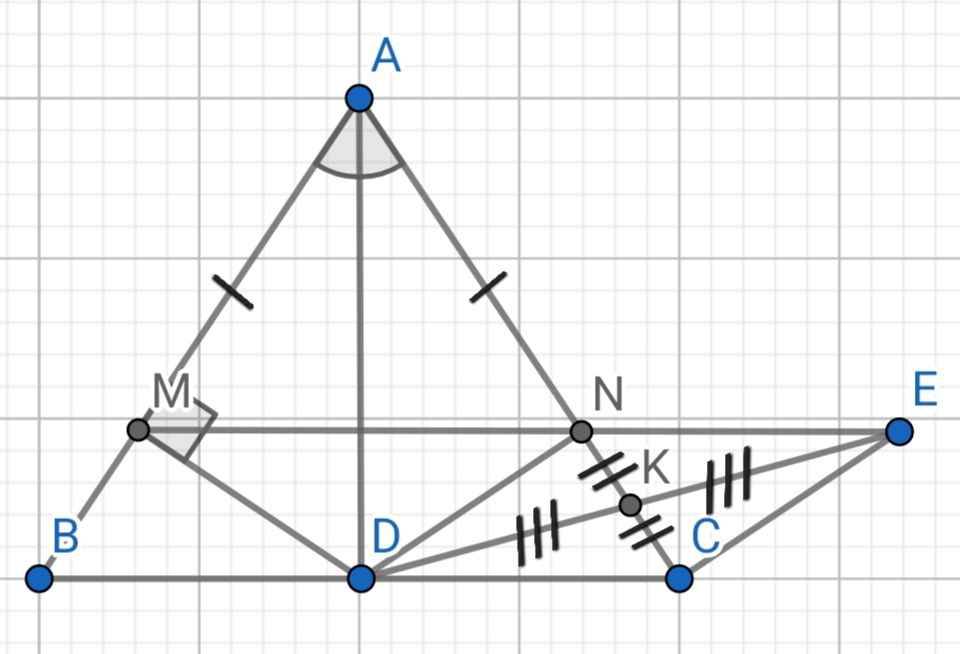a) Do AD là tia phân giác của ∠BAC (gt)
⇒ ∠BAD = ∠CAD
Do ∆ABC cân tại A
⇒ AB = AC
Xét ∆ABD và ∆ACD có:
AB = AC (cmt)
∠BAD = ∠CAD (cmt)
AD là cạnh chung
⇒ ∆ABD = ∆ACD (c-g-c)
⇒ BD = CD
⇒ D là trung điểm của BC (1)
Do ∆ABD = ∆ACD (cmt)
⇒ ∠ADB = ∠ADC (hai góc tương ứng)
Mà ∠ADB + ∠ADC = 180⁰ (kề bù)
⇒ ∠ADB = ∠ADC = 180⁰ : 2 = 90⁰
⇒ AD ⊥ BC (2)
Từ (1) và (2) ⇒ AD là đường trung trực của BC
b) Sửa đề: Chứng minh ∆ADM = ∆ADN
Do ∠BAD = ∠CAD (cmt)
⇒ ∠MAD = ∠NAD
Xét ∆ADM và ∆ADN có:
AD là cạnh chung
∠MAD = ∠NAD (cmt)
AM = AN (gt)
⇒ ∆ADM = ∆ADN (c-g-c)
⇒ ∠AMD = ∠AND = 90⁰ (hai góc tương ứng)
⇒ DN ⊥ AN
⇒ DN ⊥ AC
d) Do K là trung điểm của CN (gt)
⇒ CK = KN
Xét ∆DKC và ∆EKN có:
CK = KN (cmt)
∠DKC = ∠EKN (đối đỉnh)
KD = KE (gt)
⇒ ∆DKC = ∆EKN (c-g-c)
⇒ ∠KDC = ∠KEN (hai góc tương ứng)
Mà ∠KDC và ∠KEN là hai góc so le trong
⇒ EN // CD
⇒ EN // BC (3)
∆AMN có:
AM = AN (gt)
⇒ ∆AMN cân tại A
⇒ ∠AMN = (180⁰ - ∠MAN) : 2
= (180⁰ - ∠BAC) : 2 (4)
∆ABC cân tại A (gt)
⇒ ∠ABC = (180⁰ - ∠BAC) : 2 (5)
Từ (4) và (5) ⇒ ∠AMN = ∠ABC
Mà ∠AMN và ∠ABC là hai góc đồng vị
⇒ MN // BC (6)
Từ (3) và (6) kết hợp với tiên đề Euclide ⇒ M, N, E thẳng hàng
a: Xét ΔADK và ΔACK có
AD=AC
góc DAK=góc CAK
AK chung
=>ΔADK=ΔACK
=>DK=CK
b: ΔADC cân tại A
mà AM là phân giác
nên AM vuông góc DC
=>AM//HB
Có hình ko ạ