Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

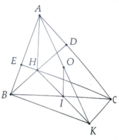
a, BHCK có I là trung điểm hai đường chéo
b, Ta có ∆ABK, ∆ACK vuông tại B và C nên A,B,K,C nằm trên đường tròn đường kính AK
c, Ta có OI là đường trung bình của ∆AHK => OI//AH
d, Gọi AH cắt BC tại M. Ta có BE.BA = BM.BC và CA.CD = CM.BC => ĐPCM

Cho tam giác ABC (AB<AC) có 2 đường chéo BD và CE cắt nhau tại H, lấy I là trung điểm BC ạ

a: Xét tứ giác BHCK có
I là trung điểm chung của BC và HK
=>BHCK là hình bình hành
b: BHCK là hbh
=>BH//CK và BK//CH
=>BK vuông góc AB và CK vuông góc CA
góc ABK=góc ACK=90 độ
=>ABKC nội tiếp đường tròn đường kính AK
=>O là trung điểm của AK
c: Xét ΔKAH có
KO/KA=KI/KH=1/2
nên OI//AH
d: gọi giao của AH với BC là F
=>AH vuông góc BC tại F
Xét ΔBEC vuông tại E và ΔBFA vuông tại F có
góc B chung
=>ΔBEC đồng dạng với ΔBFA
=>BE/BF=BC/BA
=>BE*BA=BF*BC
Xét ΔCDB vuông tại D và ΔCFA vuông tại F có
góc C chung
=>ΔCDB đồng dạng với ΔCFA
=>CD/CF=CB/CA
=>CD*CA=CF*CB
=>BE*BA+CD*CA=BC^2
ấy ấy ko làm chuyện đó ý