K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên

12 tháng 12 2021
Gọi Bx là tia đối của tia BA. Lấy E trên AC sao cho AB = AE
Xét tam giác BAD=EAD c-g-c => BD = DE và DEC = CBx
Trong tam giác ABC, BAC + ABC + ACB = 180 => ACB = 180 - BAC - ABC => ACB < 180 - ABC
Ta có DBx + ABC = 180 (hai góc kề bù) => DBx = 180 - ABC
=>ACB < DBx => ACB < DEC => Trong tam giác DEC, DC > DE (Quan hệ giữa góc và cạnh)
Vậy BD < DC
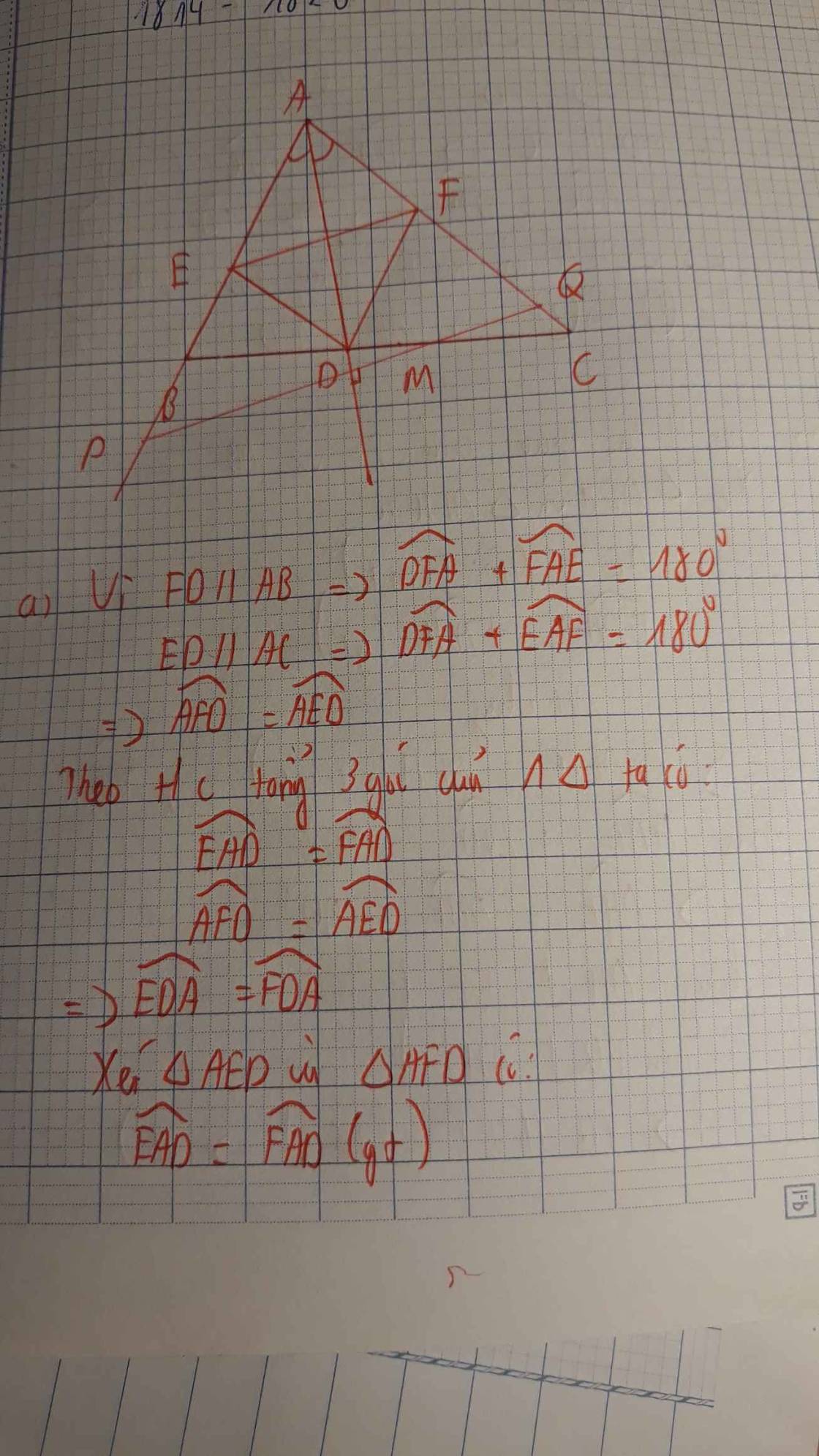


cho tam giác ABC ( AB khác AC) . tia phân giác Ax của góc A cắt BC ở D. từ D kẻ một đường thẳng song song với AB cắt AC tại F.từ D kẻ đường thẳng song song với AC cắt AB ở E.
a) CM AE=ED=DF=FA
b) từ trung điểm M của cạnh BC kẻ đường thẳng vuông góc với AC tại Pva cắt đường thẳng AB tại Q.CM EF song song với PQ.
c) CM BP=CQ