K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên

KN
24 tháng 1 2020

Theo giả thiết ta có: \(CF\perp AM\)nên \(\Delta MCF\)vuông tại F
Suy ra CF < MC (cạnh góc vuông bé hơn cạnh huyền) (1)
Tương tự ta có: BE < BM (2)
Từ (1) và (2) suy ra \(BE+CF< BM+MC=BC\)
Vậy \(BE+CF< BC\left(đpcm\right)\)

CM
12 tháng 10 2019
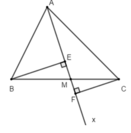
Vì BE ⊥ Ax tại E nên tam giác BEM vuông tại E ⇒ BM > BE (quan hệ đường xiên và đường vuông góc)
Vì CF ⊥ Ax tại F nên tam giác CFM vuông tại F ⇒ CM > CF (quan hệ đường xiên và đường vuông góc)
Khi đó ta có: BM + CM > BE + CF
Mà BM + CM = BC (M thuộc BC)
Do đó: BC > BE + CF hay BE + CF < BC.
Chọn đáp án A