Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

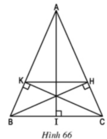
a) Xét 2 tam giác vuông: \(\Delta KBC\) và \(\Delta HCB\)
\(\widehat{KBC}=\widehat{HCB}\)
\(BC\) chung
suy ra: \(\Delta KBC=\Delta HCB\)(ch_gn)
\(\Rightarrow\)\(BK=CH\)
b) \(AB=AC\) VÀ \(BK=CH\)
\(\Rightarrow\)\(\frac{BK}{AB}=\frac{HC}{AC}\)
\(\Rightarrow\) \(KH//BC\) (theo định lý Ta-lét đảo)

A B C H K I
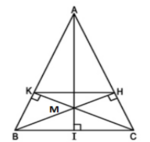
a, tg ABC cân tại A (gt) => ^ABC = ^ACB (tc)
xét tg HCB và tg KBC có : BC chung
^CHB = ^BKC = 90
=> tg ABC = tg KBC (ch-gn)
=> CH = BK (đn)
=> CH/AB = BK/AB mà AB = AC do tam giác ABC cân tại A (Gt)
=> CH/AC = BK/AB
=> HK // BC (đl)
b, sửa đề thành HC.AC = BC.IC
xét tg CHB và tg CIA có : ^ACB chung
^CHB = ^AIC = 90
=> tg CHB đồng dạng với tg AIC (g-g)
=> HC/BC = IC/AC (đn) => HC.AC = BC.IC
c, tg ABC cân tại A (Gt) mà AI là đường cao (gt)
=> AI đồng thời là đtt (đl) => IB = IC = 1/2 BC
mà có : HC.AC = BC.IC (Câu b) ; BC = a; AC = b
=> HC.b = a.a/2 => BC = a^2/2b
Có AH = AC - HC
=> AH = b - a^2/2b = (2b^2 - a^2)/2b
mà HK // BC (câu a) nên
AH/AC = HK/BC => HK = AH.BC/AC = a/b.(2b^2 - a^2)/2b
=> HK = (2ab^2 - a^3)/2b^2 = a - a^3/2b^2

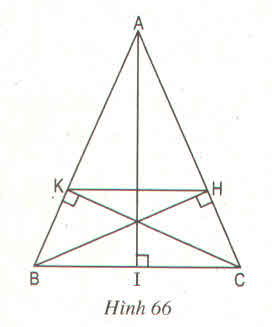
a) Xét tam giác BKC và CHB có:
góc B= góc C (tính chất tam giác cân)
góc BKC = góc BHC = 90 độ
=> Tam giác BKC đồng dạng tam giác CHB
=> \(\frac{BK}{CH}=\frac{BC}{BC}=1=k\)
b) Tam giác BHA đồng dạng tam giác CKA (g-g)
=> \(\frac{HA}{AK}=\frac{BA}{AC}=1\)
=> \(\frac{AK}{AB}=\frac{AH}{AC}\)
=> KH//BC (Định lí Ta - lét đảo)
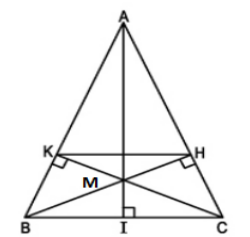
c) Ta có theo hệ quả Ta-let:
\(\frac{AK}{AB}=\frac{KH}{BC}=>\frac{AK}{b}=\frac{KH}{a}=>KH=\frac{a.AK}{b}\)
Ta có: AK2+KC2=b2 (1)
KC2+KB2=a2 => KC2+(b-AK)2=a2 =>KC2-2b.AK+AK2=a2 (2)
Trừ 2 cho 1, ta có: -2b.AK=a2-b2 =>\(AK=\frac{a^2-b^2}{-2b}\)
Từ đó => \(KH=\frac{a\times\frac{a^2-b^2}{-2b}}{b}\)