Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Lời giải:

a) Vì $BD, CE$ là đường cao nên \(BD\perp AC, CE\perp AB\)
\(\Rightarrow \widehat{HDA}=\widehat{HEA}=90^0\)
\(\Rightarrow \widehat{HDA}+\widehat{HEA}=180^0\)
Do đó tứ giác $ADHE$ nội tiếp.
Gọi $I$ là trung điểm của $AH$ thì \(AI=IH=\frac{AH}{2}\)
Xét tam giác $AEH$ vuông tại $E$ có $I$ là trung điểm cạnh huyền $AH$ nên \(EI=\frac{AH}{2}\) (theo định lý về đường trung tuyến đối diện cạnh huyền của tam giác vuông).
Hoàn toàn tương tự \(DI=\frac{AH}{2}\)
Do đó: \(AI=HI=EI=DI\Rightarrow I\) là tâm đường tròn ngoại tiếp tứ giác $ADHE$
b)
Vì ba đường cao của tam giác thì đồng quy tại một điểm nên hiển nhiên $AF$ là đường cao của tam giác $ABC$
\(\Rightarrow \widehat{ADB}=\widehat{AFB}=90^0\)
\(\Rightarrow ADFB\) nội tiếp.
\(\Rightarrow \widehat{DAB}+\widehat{DFB}=180^0\) (hai góc đối nhau)
Mà \(\widehat{DFB}+\widehat{DFC}=180^0\Rightarrow \widehat{DAB}=\widehat{DFC}(1)\)
Lại có: \(\widehat{DAB}=\widehat{BCx}\) (cùng chắn cung BC)
Do đó: \(\widehat{DFC}=\widehat{BCx}\), mà hai góc này ở vị trí so le trong nên \(Cx\parallel DF\)
Ta có đpcm.

d)
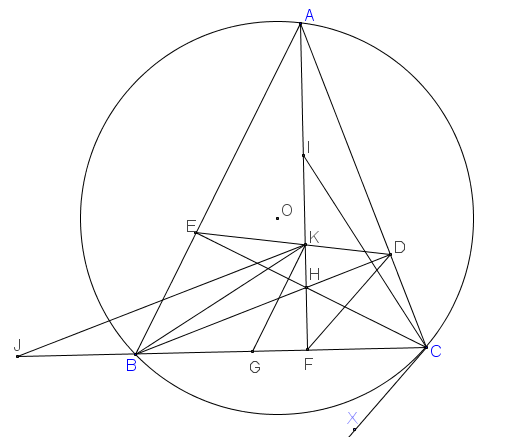
Trên BF lấy điểm G sao cho GK //AB
=>KG⊥⊥CE (1) và BGBF=AKAFBGBF=AKAF (2)
theo câu c), DH là phân giác trong ˆKDFKDF^ (3)
=>HKHF=DKDFHKHF=DKDF (4)
có DA⊥⊥DH (5)
từ (3, 5) =>DA là phân giác ngoài ˆKDFKDF^
=>AKAF=DKDFAKAF=DKDF (6)
từ (2, 4, 6) =>BGBF=HKHFBGBF=HKHF (7)
trên tia đối tia BC lấy điểm J sao cho BJ =BG
=>BJBF=BGBFBJBF=BGBF (8)
từ (7, 8) =>BJBF=HKHFBJBF=HKHF
=>JK // BH
=>JK⊥⊥AC (8)
từ (1, 8) =>ˆJKG=ˆACHJKG^=ACH^ (9)
và có JF⊥⊥AH và (1)=>ˆKGJ=ˆCHAKGJ^=CHA^ (10)
từ (9, 10) =>△KGJ∼△CHA△KGJ∼△CHA (g, g)
=>KGCH=GJHA=2.GB2.HI=GBHIKGCH=GJHA=2.GB2.HI=GBHI (11)
từ (10, 11) =>△KGB∼△CHI△KGB∼△CHI (c, g, c)
=>ˆKBF=ˆCIFKBF^=CIF^
=>△FBK∼△FIC△FBK∼△FIC (đpcm)
và ˆICB+ˆFBKICB^+FBK^
=ˆBKF+ˆFBK=90∘=BKF^+FBK^=90∘
=>BK⊥CIBK⊥CI =>K là trực tâm của tam giác IBC (đpcm)
Hình gửi kèm

B1, a, Xét tứ giác AEHF có: góc AFH = 90o ( góc nội tiếp chắn nửa đường tròn)
góc AEH = 90o (góc nội tiếp chắn nửa đường tròn )
Góc CAB = 90o ( tam giác ABC vuông tại A)
=> tứ giác AEHF là hcn(đpcm)
b, do AEHF là hcn => cũng là tứ giác nội tiếp => góc AEF = góc AHF ( hia góc nội tiếp cùng chắn cung AF)
mà góc AHF = góc ACB ( cùng phụ với góc FHC)
=> góc AEF = góc ACB => theo góc ngoài tứ giác thì tứ giác BEFC là tứ giác nội tiếp (đpcm)
c,gọi M là giao điểm của AI và EF
ta có:góc AEF = góc ACB (c.m.t) (1)
do tam giác ABC vuông tại A và có I là trung điểm của cạng huyền CB => CBI=IB=IA
hay tam giác IAB cân tại I => góc MAE = góc ABC (2)
mà góc ACB + góc ABC + góc BAC = 180o (tổng 3 góc trong một tam giác)
=> ACB + góc ABC = 90o (3)
từ (1) (2) và (3) => góc AEF + góc MAE = 90o
=> góc AME = 90o (theo tổng 3 góc trong một tam giác)
hay AI uông góc với EF (đpcm)